Уравнение для этих случаев принимает вид
k = 0 ао(0)y2 + а1(0)y1 + а2(0)yо = хо;
k = 1 ао(1)y2 + а1(1)y1 + а2(1)yо = х1;
k = 2 ао(2)y2 + а1(2)y1 + а2(2)yо = х2.
Отсюда можем определить коэффициенты аi. Сначала ао (рис.15.14), а затем а1 и а2.
Рассмотренная ДМ применяется для анализа непрерывных ОД.
Специальные диагностические модели. Эти модели разделяются на информационные и функциональные.
Информационные ДМ разрабатываются на объекты, которые могут быть заданы функционально конструктивными блоками представлять собой описание информационных потоков, циркулирующих в оборудовании.
В этом случае диагностируемое оборудование рассматривается как преобразователь информации. Каждый элемент объекта (информационный узел) представляется источником или преобразователем информации (рис.15.15). Оценивается поток этой информации.
Уравнение динамики для информационного узла имеет вид:
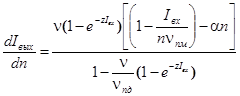 ,
,
где Iвх – поток входной информации; Iвых – поток выходной информации; n – число информационных элементов в информационном узле; 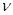 – максимальная производительность; z – коэффициент, характеризующий затраты выходной информации на единицу входной информации;
– максимальная производительность; z – коэффициент, характеризующий затраты выходной информации на единицу входной информации; 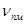 – производительность приема информации;
– производительность приема информации; 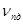 – производительность передачи информации;
– производительность передачи информации; 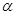 – доля потока информации затрачиваемая на согласование.
– доля потока информации затрачиваемая на согласование.
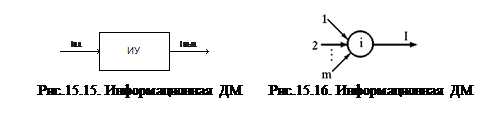 Анализируя уравнение, можно определить количество информационных элементов, обеспечивающих максимальную производительность узла, и, в конечном счете, ОД с учетом состояния параметров.
Анализируя уравнение, можно определить количество информационных элементов, обеспечивающих максимальную производительность узла, и, в конечном счете, ОД с учетом состояния параметров.
К информационным диагностическим моделям относятся также и описания, представляющие собой информационную оценку изменения состояния оборудования. Информация о состоянии каждой структурной единицы (рис.15.16) может быть определена с помощью выражения:
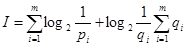 ,
,
где qi = 1-pi (pi – вероятность появления сигнала на выходе СЕ с учетом ее структуры); m – число входов.
Информационные модели наиболее универсальные, поскольку не зависят от принципа построения и действия оборудования.
Функциональные ДМ отражают совокупность операций, выполняемых оборудованием и его отдельными частями (структурными единицами) в процессе функционирования. В качестве функциональных моделей могут рассматриваться схемы связей между отдельными СЕ, диаграммы прохождения сигналов (ориентированные графы) или алгоритмы функционирования.
Диагностическая модель в виде схемы связей представляет собой объединение СЕ, имеющих много входов и только один выход (рис.15.17).
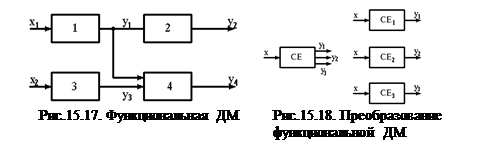
В этом случае оценивается состояние каждой СЕ двумя состояниями: 0 – неработоспособна, 1 – работоспособна. Для рассматриваемого примера работоспособное состояние ОД можно записать в виде Sp = (1111). Состояние каждой СЕ определяется соответствующей проверкой при подаче на ОД всех входных воздействий.
Если СЕ имеет несколько выходов, то она разбивается на число СЕ, равное числу выходов (рис.15.18). В дальнейшем такая ДМ используется для анализа с помощью таблиц состояний.
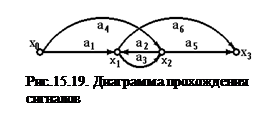
Для анализа ОД широко применяются диаграммы прохождения сигналов, которые являются графическим представлением системы линейных алгебраических уравнений. В таком представлении вершины - переменные, а ветви - коэффициенты.
Например, система алгебраических уравнений
х1 = а1хо + а2х2;
х2 = а3х1 + а4хо;
х3 = а5х2 + а6х1.
может быть представлена в виде диаграммы прохождения сигналов (рис.15.19).
Такое представление позволяет за счет существующих правил преобразовать диаграмму прохождения сигналов и упростить исходную систему уравнений, а также использовать непосредственно для анализа с привлечением аппарата теории чувствительности.
 В случае использования в качестве ДМ алгоритма функционирования, под которым понимается последовательность действий при решении поставленной задачи, анализу может подвергаться последовательность и время выполнения операций.
В случае использования в качестве ДМ алгоритма функционирования, под которым понимается последовательность действий при решении поставленной задачи, анализу может подвергаться последовательность и время выполнения операций.
Как ДМ могут применяться характеристики электрооборудования статические и динамические (временные и частотные).
Различные виды ДМ используются как самостоятельно, так и в различных сочетаниях в зависимости от условий, в которых разрабатывается диагностическое обеспечение, и специфики конкретного электрооборудования.
Дата добавления: 2015-06-10; просмотров: 693;
