Способы построения диагностических моделей
Способ построения ДМ во многом определяется видом модели. В связи с большим разнообразием ДМ электрооборудования существует множество различных способов их построения. Однако эти способы можно сгруппировать, учитывая их направленность и особенности. Так, при построении непрерывной ДМ предусматривается большое число способов упрощения дифференциального или алгебраического сравнения высокого порядка, описывающего диагностируемое оборудование, до порядка, позволяющего описывать процессы с допустимой погрешностью.
Упрощение передаточной функции.Если оборудование описывается передаточной функцией вида:
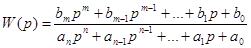 ,
,
то ДМ может быть получена разложением передаточной функции (15.1) в цепную дробь по следующей процедуре:
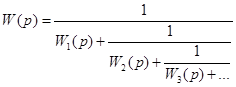 ,
,
где составляющие Wi(p) определяются в результате деления полинома на полином в следующей последовательности:
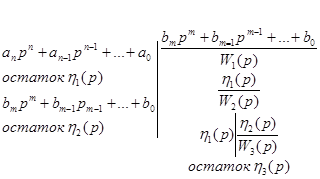
и.т.д.
На каждом шаге разложения передаточной функции в цепную дробь можно оценить получаемую погрешность, если в качестве ДМ использовать полученные выражения, отбросив остаток:
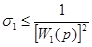 ;
; 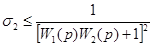 ;
;
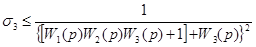 и.т.д.
и.т.д.
Пример. Оборудование описывается передаточной функцией вида
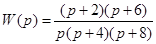 . (15.3)
. (15.3)
Построить ДМ, разложив передаточную функцию в цепную дробь, сделав два шага, и оценить погрешность при отбрасывании остатка на каждом шаге.
Представим числитель и знаменатель выражения (15.3) в виде полиномов
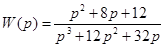
Произведем соответствующие операции деления:
1-й шаг
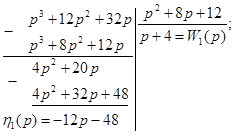
2-й шаг
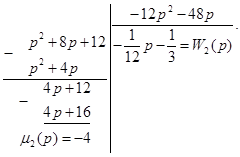
Получим в соответствии с (15.2) передаточную функцию
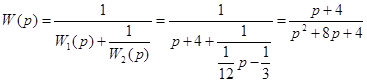 ,
,
которую и будем рассматривать как ДМ. Погрешность, допускаемая при этом, будет
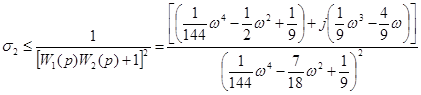 .
.
Соответственно, погрешность по модулю будет
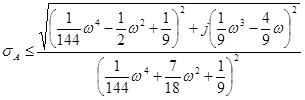
и по фазе
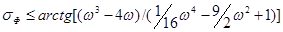 .
.
Рассчитаем 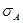 и
и 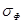 для различных
для различных 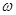 :
:
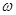 ,с-1...0 ,с-1...0
| 0,2 | 0,47 | 1,0 | 2,0 | 4,0 | 8,45 | 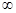
| ||
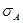 ...9 ...9
| - | - | 0,56 | - | - | 0,01 | - | ||
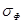 ...0 ...0
| -41 | 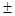 90 90
| +41 | -41 | 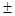 90 90
| +80 | +9 |
Графические зависимости для этих данных 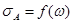 и
и 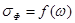 приведены на рис.15.20.
приведены на рис.15.20.
Усечение характеристического уравнения. 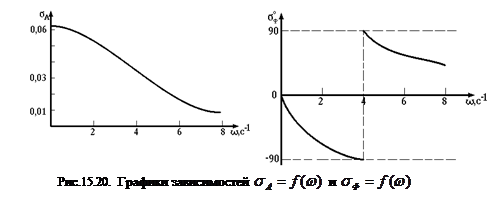
Если характеристическое уравнение, описывающее оборудование, имеет высокий порядок, то в качестве ДМ можно использовать упрощенное характеристическое уравнение, получаемое усечением исходного, т.е. исключением из рассмотрения некоторых его членов. При этом рассматривается процесс построения последовательности хi, 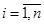 , сходящейся к корню х полного характеристического уравнения f(x) = 0. В качестве нулевого приближения берется корень усеченного уравнения
, сходящейся к корню х полного характеристического уравнения f(x) = 0. В качестве нулевого приближения берется корень усеченного уравнения 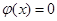 . Если такой процесс сходится к корню уравнения f(x) = 0 и возможна оценка погрешности его приближения, то уравнение
. Если такой процесс сходится к корню уравнения f(x) = 0 и возможна оценка погрешности его приближения, то уравнение 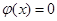 можно использовать как ДМ.
можно использовать как ДМ.
При построении модели применяется итерационный способ Ньютона, дающий следующие формальные итерации:
хо – произвольное число;
х1 = хо – f(xо)/f'(xо);
хn+1 = хn – f(xn)/f'(xn).
Доказано, что если xо – корень уравнения 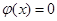 и существует такое число
и существует такое число  >0 (не отрицательное), что в окружности радиуса
>0 (не отрицательное), что в окружности радиуса 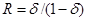 число
число 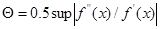 удовлетворяет неравенству,
удовлетворяет неравенству, 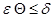 ;
; 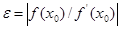 , то существует х – корень уравнения f(x)=0 такой, что
, то существует х – корень уравнения f(x)=0 такой, что 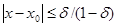 .
.
Таким образом, соблюдение этого условия означает возможность приближения с точностью  корня х полного характеристического уравнения f(x) = 0 к корню xо усеченного уравнения f(x) = 0. При этом, если корни x1,х2,...,хn малы, то усечение нужно осуществлять слева, а если велики, то справа.
корня х полного характеристического уравнения f(x) = 0 к корню xо усеченного уравнения f(x) = 0. При этом, если корни x1,х2,...,хn малы, то усечение нужно осуществлять слева, а если велики, то справа.
Пример.Оборудование описывается дифференциальным уравнением, которое имеет характеристическое уравнение:
р3 + 4,9р2 + 6,5р - 0,7 = 0
Корни характеристического уравнения соответственно равны
р1 = 0,1; р2,3 = 2,45 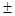 0.7, a
0.7, a  = 0.2.
= 0.2.
Необходимо построить ДМ оборудования, усекая характеристическое уравнение. Ориентироваться при этом нужно на большие корни, т.е. усекать уравнение справа.
Устранив один член из характеристического уравнения справа, получим усеченное уравнение:
р2 + 4,9р + 6,5 =Q.
Для определения 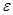 и
и 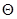 возьмем производные
возьмем производные
f'(p) = 3p2 + 9,8p + 6,5; f"(p) = 6p + 9,8.
Тогда
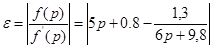
После разложения по степеням р-ро (ро=хо), получим:
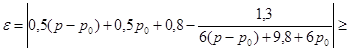
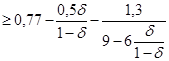 .
.
Дата добавления: 2015-06-10; просмотров: 1266;
