Способы преобразования чертежа

Общая характеристика способов преобразования чертежа

Решение пространственных задач на комплексном чертеже значительно упрощается, если интересующие нас элементы пространства занимают частное положение. Достигается это методами преобразования чертежа. Так как частных положений у прямой два н у плоскости два, то существует четыре исходных задачи для преобразования:

1) прямую общего положения сделать прямой уровня;

2) прямую уровня сделать проецирующей,

3) плоскость общего положения сделать проецирующей плоскостью;

4) проецирующую плоскость сделать плоскостью уровня.

Преобразование чертежа отображает изменение положения геометрических образов или плоскостей проеций в пространстве. Чаще всего применяют способ замены плоскостей и способ вращения.

Способ замены плоскостей

Сущность способа замены плоскостей состоит в том, что пространственное положение объектов пространства остается неизменным, а меняется система плоскостей проекций путем ввода дополнительных плоскостей проекций, при этом сохраняется взаимная перпендикулярность двух плоскостей проекций. На дополнительные плоскости проекций строятся новые изображения геометрических образов. Дополнительные плоскости выбираются таким образом, чтобы на них интересующие нас элементы изображались в удобном для конкретной задачи положении. Все свойства геометрического образа, отнесенные к основной системе, справедливы и для новой системы плоскостей проекций.

Оси проекций будем отмечать в виде дроби, считая, что черта лежит на этой оси Обозначение плоскостей представляет собой как бы числитель и знаменатель дроби, причем каждая буква ставится на ту сторону оси, где должны размещаться соответствующие проекции, например:

Пусть заданы точка А и система х 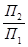— ортогональными проекциями точки А на эти плоскости будут а₁ и A₂. Возьмем новую плоскость П₁^ П₂ и спроецируем точку А на эту плоскость; проекцией будет А₄ (рис. 28)

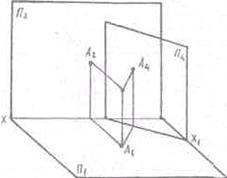
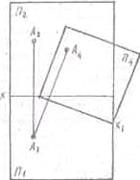
Рис.28.

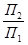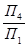Плоскость П₁ входит в обе системы х и х . Поэтому а₁ относится и к системе х 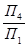.При проецировании точки на П₄ получаем А₄ на расстоянии равном Z_а. Последовательный переход от одной системы плоскостей проекции к другой необходимо осуществлять, выполняя следующее правило. Расстояние от новой проекции точки до новой оси должно равняться расстоянию от заменяемой проекции точки до предыдущей оси.

Если введение одной плоскости не решает задачи, прибегают к последовательному дополнению основной системы плоскостей проекций новыми.

При решении четырех исходных задач выполняют следующее:

- для первой - дополнительную плоскость выбирают параллельно заданной прямой общего положения;

- для второй - дополнительную плоскость выбирают перпендикулярно заданной прямой уровня;

- для третьей - в заданной плоскости общего положения построить линию уровня и дополнительную плоскость выбирают перпендикулярно ей;

- для четвертой - дополнительную плоскость выбирают параллельно проецирующей плоскости.