Построение взаимно перпендикулярных прямой и плоскости

Из всех возможных положений прямой, пересекающей плоскости, отметим случай, когда прямая перпендикулярна к плоскости.

Прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым, лежащим в данной плоскости. Поэтому, чтобы построить перпендикуляр к плоскости берут две прямые - горизонталь и фронталь в данной плоскости, т.к. перпендикуляр с этими прямыми образует угол равный - 90°

У перпендикуляра к плоскости его горизонтальная проекция перпендикулярна к горизонтальной проекции горизонтали, фронтальная проекция перпендикулярна к фронтальной проекции фронтали, профильная проекция перпендикулярна к профильной проекции профильной прямой этой плоскости. (Рис.24)

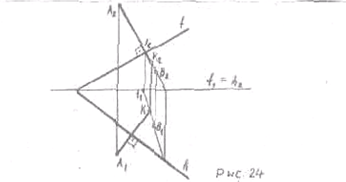В случае задания плоскости следами, если прямая перпендикулярна к плоскости, то горизонтальная проекция этой прямой перпендикулярна к горизонтальному следу плоскости, а фронтальная проекция перпендикулярна к фронтальному следу плоскости. (Рис.25)

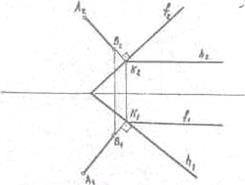
Рис. 25

Т.к перпендикуляр к плоскости перпендикулярен к любой прямой, проведенной в этой плоскости, можно воспользоваться этим для проведения перпендикуляра из некоторой точки А к прямой общего положения ВС.

1. через точку А провести плоскость/Г/, перпендикулярную к прямой ВС

2. определить точку К пересечения прямой ВС с плоскостью Г

3. соединить точки А и К отрезком прямой линии. Прямые АК и ВС взаимно перпендикулярны.