Операции наращения капитала

Известны две основные схемы дискретного начисления:

• схема простых процентов (simple interest);

• схема сложных процентов (compound interest).

Схема простых процентов предполагает неизменность базы, с ко­торой происходит начисление. Пусть исходный инвестируемый ка­питал равен Р; требуемая доходность — r (в долях единицы). Счи­тается, что инвестиция сделана на условиях простого процента, если инвестированный капитал ежегодно увеличивается на величину P · r. Таким образом, размер инвестированного капитала (R_n) через п лет будет равен:

R_n = P + P · r + … + P · r = P · (1 + n ·r)

Считается, что инвестиция сделана на условиях сложного про­цента, если очередной годовой доход исчисляется не с исходной ве­личины инвестированного капитала, а с общей суммы, включающей также и ранее начисленные и не востребованные инвестором про­центы. В этом случае происходит капитализация процентов по мере их начисления, т.е. база, с которой начисляются проценты, все время возрастает. Следовательно, размер инвестированного капитала будет равен:

к концу первого года: F₁ = P + P · r = P · (1 + r);

к концу второго года: F₂ = F₁ + F₁ · r = F₁ · (1 + r) = P · (1 + r)²;

….

к концу n – го года: F_n = P · (1 + r)ⁿ.

Как же соотносятся величины R_n и F_n. Это чрезвычайно важно знать при проведении финансовых операций. Все зависит от величи­ны п. Сравним множители наращения по простым и сложным про­центам, т.е. сравним: 1 + п · r и (1 + r)ⁿ. Очевидно, что при п = 1 эти множители совпадают и равны 1 + r. Можно показать, что при лю­бом r справедливы неравенства: 1+ п · r >(1 + r)ⁿ, если 0 < п < 1 и 1 + п · r < (1 + r)ⁿ , если п > 1. Итак,

- R_n > F_n при 0 < п< 1;

- R_n < F_n при п >1.

Графически взаимосвязь F_n и R_n можно представить следующим образом (рис. .2).

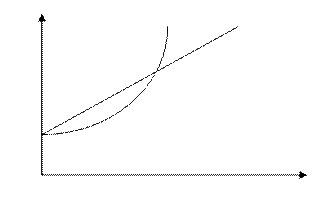
Рис. 2. Схема простых и сложных процентов

Таким образом, в случае ежегодного начисления процентов для лица, предоставляющего кредит:

• более выгодной является схема простых процентов, если срок ссудыменее одного года (проценты начисляются однократно в конце периода);

• более выгодной является схема сложных процентов, если срок ссуды превышает один год (проценты начисляются ежегодно);

• обе схемы дают одинаковые результаты при продолжительнос­ти периода один год и однократном начислении процентов.

Формула сложных процентов является одной из базовых формуле финансовых вычислениях, поэтому для удобства пользования значе­ния множителя FM1(r,n) называемого мультиплицирующим множи­телем для единичного платежа и обеспечивающего наращение сто­имости, табулированы для различных значений r и п.