Проектирование зубчатых механизмов
§1 Кинематический анализ передач
Передаточным отношением называется отношение угловых скоростей зубчатых колес (или числа оборотов):
U12 = ω1/ω2 = n1 / n2. (5.1)
Задачей кинематического анализа передач является нахождение передаточного отношения передачи через отношения размерных параметров ее звеньев.
Различают одноступенчатые передачи, такие, в которых имеются только два звена с неподвижными осями вращения, и многоступенчатые, в которых звеньев с неподвижными осями вращения больше двух.
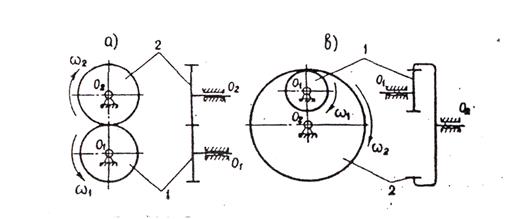
а – внешнее зацепление; б – внутреннее зацепление
Рисунок 5.1. - Схемы зацеплений зубчатых колес
Рассмотрим одноступенчатые передачи. Для внешнего зацепления (рисунок 5.1, а) передаточное отношение имеет отрицательный знак, т.к. колеса вращаются в разные стороны
U12= - ω1/ω2.
Для внутреннего зацепления (рисунок 5.1, б) передаточное отношение имеет положительный знак, т.к. угловые скорости колес направлены в одну сторону
U12= + ω1/ω2.
Передаточное отношение можно определять также через отношение чисел зубьев z колес, которыми обычно и задаются:
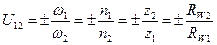, (5.2)
где n – число оборотов, RW – радиус начальной окружности.
Для передачи с коническими колесами (рисунок 5.2, а)
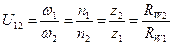. (5.3)
Для червячной передачи (рисунок 5.2, б)
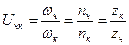, (5.4)
где zк – число зубьев на колесе, zч – число заходов на червяке. Передаточное отношение конической и червячной передач не имеют знака, т.к. оси их не параллельны.
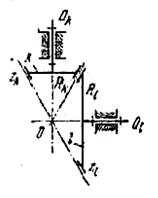
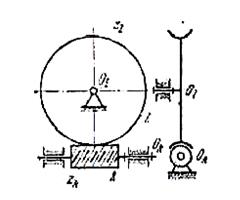
а(34) – коническая передача; б(35) – червячная передача
Рисунок 5.2. – Пространственные передачи
Многоступенчатые передачи конструируются таким образом, что передача угловой скорости (числа оборотов) от звена 1 к звену n, имеющих неподвижные оси вращения, осуществляется через несколько промежуточных звеньев.
Передаточное отношение многоступенчатого зубчатого механизма есть произведениевзятых со своими знаками передаточных отношений отдельных его ступеней, т.е.:
U1n= (-1)kU12×U23×U34×…·U(n-1)n. (5.5)
где k – число внешних зацеплений. Множитель (-1)k позволяет определить знак передаточного отношения сложного зубчатого механизма.
Ступень передачи – контакт (зацепление) двух колес.
§2 Определение размеров цилиндрических редукторов
Профили двух круглых колес, которые соприкасаются в точке полюса р и перекатываются без скольжения, называются начальными окружностями. Радиусы этих окружностей обозначаются RW1 и RW2. Тогда межосевое расстояние aW
aW = [О1О2] = RW1 + RW2. (5.6)
Высота зуба h колеса состоит из головки зуба ha и ножки зуба hf:
h = ha+ hf. (5.7)
Окружность, которая делит зуб на головку и ножку, называетсяделительной. Ее радиус обозначается R и вычисляется по формуле:
R = mz/2 (мм), (5.8)
где z1, z2 - число зубьев шестерни и колеса; m - модуль зацепления.
Модуль – основная характеристика размеров зубчатых и червячных колес. Модули эвольвентных зубчатых колес стандартизованы ГОСТ 9563-60. Для колес, входящих в зацепление, модуль всегда одинаков!
Модуль – это отношение шага Р к числу π
m = P/ π = (мм). (5.9)
Расстояние по делительной окружности между одноименными точками двух соседних зубьев называется шагом зацепления Р
P = π m = (мм). (5.10)
Шаг также складывается из толщины зуба и ширины впадины
P = S + e= (мм), (5.11)
где S - толщина зуба по делительной окружности, е - ширина впадины. Так как шаг измеряется в мм, поэтому и модуль имеет размерность в мм.
Для стандартного (нулевого) зацепления высота головки зуба равна модулю: ha = m, а высота ножки зуба равна hf = 1,25m.
Тогда высота зуба будет равна
h =2,25m.
Радиус, ограничивающий головку зуба, называется радиусом окружности выступов Ra
Ra= R + m. (5.12)
Развертываемая окружность, с которой начинается построение эвольвенты, называется основнойRb
Rb = Rcosα. (5.13)
где α - угол зацепления (α = 20о).
Радиус, ограничивающий впадину колеса, называется радиусом окружности впадинRf
Rf= R - 1,25m, (5.14)
Для стандартного (нулевого) зацепления радиус начальной окружности совпадает с радиусом делительной (RW=R), толщина зуба равна ширине впадины и равна половине шага (S = e = P /2) и, как указывалось выше, высота головки зуба равна модулю (ha=m), угол зацепления равен α = 20о.
Рассмотрим примеры на определение передаточного отношения для различных редукторов.
Пример 1. Рассчитать передаточное отношение от первого колеса к пятому (от ведущего к ведомому) U14 для простого рядового соединения – зубчатые колеса расположены в один ряд (рисунок 5.3).
Исходные данные. Числа зубьев колес z1=18, z2=26, z3=32 и z4=42.
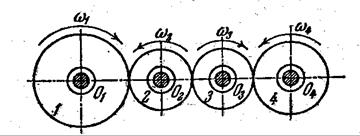
Рисунок 5.3. - Простое рядовое соединение
Решение. Количество ступеней (контактов) для данного соединения будет k =3. По формуле (5.5) имеем:
U15 = (-1)3 U12×U23×U34. (5.15)
Для каждой пары колес передаточное отношение определится по формуле (5.4), а именно:
U12 = z2/z1, U23 = z3/z2, U34 = z4/z3.
Подставив эти значения в формулу (5.13), получим:
U14 = (-) 
.
После сокращения, имеем:
.
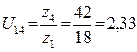Пример 2. Рассчитать передаточное отношение U13 ступенчатого соединения (рисунок 5.4) и межосевые расстояния аW1 и аW2.
Исходные данные. Числа зубьев колес z1=18, z2=26, z2’=32 и z3=42, модуль m = 8 мм, колеса считать нулевыми.
Решение. 1) Расчет передаточного отношения. Количество ступеней (контактов) для данного соединения будет k = 2. Представим передаточное отношение через произведение передаточных отношений каждой ступени (см. формулу 5.5):
U13 = (-1)2 U12×U2’3.
|
Число внешних зацеплений будет равно двум, поэтому знак передаточного отношения получится положительный. Через числа зубьев имеем:
.
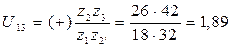2) Расчет межосевых расстояний. По формуле (5.6) имеем
aW1 = [О1О2] = RW1 + RW2.
Так как колеса являются нулевыми, то RW=R. Тогда
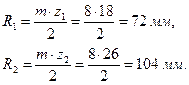
Тогда расстояние между центрами 1-го и 2-го колес
aW1 == R1 + R2= 72 + 104 = 176 мм.
2-ое межосевое расстояние рассчитывается аналогично, т.е.
.
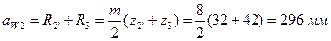Дата добавления: 2015-06-01; просмотров: 1455;