Примеры на определение КПД.

Пример 1. Определить КПД наклонной плоскости, по которой движется равномерно вверх ползун, нагруженной вертикальной силой Q; движущая сила Р параллельна основанию х-х наклонной плоскости (рисунок 4.16).

Исходные данные. Коэффициент трения ползуна о плоскость f=0,3; угол наклона плоскости α=30^о.

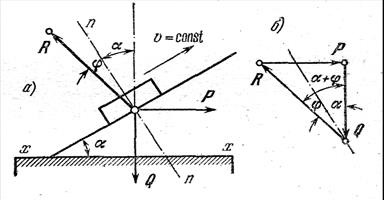
Рисунок 4.16. – Определение КПД наклонной плоскости

Решение. В данном примере сила Q является силой полезного сопротивления. Найдем соотношение между движущей силой Р и силой полезного сопротивления Q, для чего рассмотрим равновесие ползуна. К ползуну (рисунок 4.16, а) приложены сила Р, сила Q и реакция плоскости R, отклоненная от нормали n-n на угол трения

φ = arctg f =arctg 0,3 = 18^о20'.

Запишем условие равновесия ползуна

Р + Q + R = 0.

На рисунке 4.16,б построен соответствующий треугольник сил. Из него получаем

P = Q tg (α + φ)/

Пусть ползун переместиться вверх на величину S, тогда работа силы полезного сопротивления будет равна

А_пс = Q·S·sinα,

А работа движущей силы будет равна

А_дв = Р·S·cosα.

Коэффициент полезного действия найдется по формуле (4.16)

.

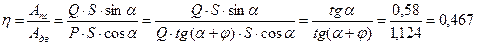Пример 2. Определить коэффициент полезного действия одноступенчатого планетарного редуктора типа Джемса (рисунок 4.17), у которого ведущим является вал О₁ колеса 1, а ведомым – вал О_Н водила Н.

Исходные данные. Число зубьев колес z₁=20, z₂=20, z₃=60. КПД каждой пары колес η=0,95.

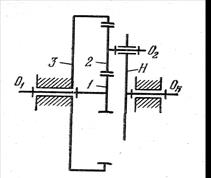
Рисунок 4.17. – Определение КПД одноступенчатого планетарного редуктора

Решение. 1. Определяем передаточное отношение одноступенчатого планетарного редуктора

.

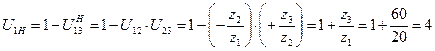2. Определяем коэффициент полезного действия обращенного механизма. По формуле (4.19) имеем

.

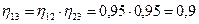3. Находим искомый коэффициент полезного действия редуктора. Так как U_1H больше единицы, то воспользуемся формулой (4.21)

.

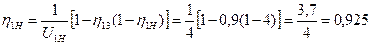Следует обратить внимание, что найденный коэффициент полезного действия редуктора больше КПД обращенного механизма.