ЗАДАЧИ 104-109
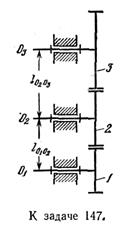
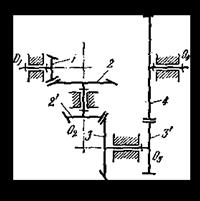
Задача 104. Определить передаточное отношение U13, а также расстояния между осями ℓО1О2 и ℓО2О3 цилиндрического однорядного редуктора. Исходные данные. Модуль зубчатой передачи m = 10 мм, числа зубьев колес z1 = 20, z2 = 30, z3 = 40.
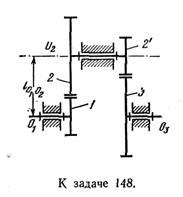
Задача 105. Определить передаточное отношение U13, а также расстояния между осями ℓО1О2 цилиндрического ступенчатого редуктора. Исходные данные. Модуль зубчатой передачи m = 10 мм, числа зубьев колес z1 = 20, z2 = 40, z'2 = 15, z3 = 45.
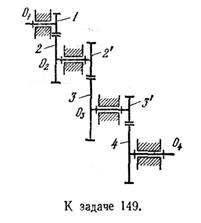
Задача 106. Определить передаточное отношение U14 цилиндрического ступенчатого редуктора. Исходные данные. Числа зубьев колес z1 = 16, z2 = 48, z'2 = 20, z3 = 40, z'3 = 13, z4 = 26.
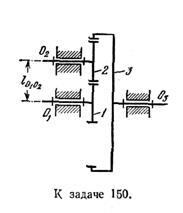
Задача 107. Определить передаточное отношение U13, а также расстояние между осями ℓО1О2 зубчатой передачи. Исходные данные. Модуль зубчатой передачи m = 12 мм, числа зубьев колес z1 = z2 = 20, z3 = 60.
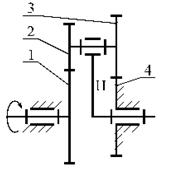
Задача 108. Определить передаточное отношение U14 зубчатой передачи. Исходные данные. Числа зубьев колес z1 = 20, z2 = 40, z'2 = 20, z3 = 30, z'3 = 20, z4 = 40. Ничего не меняя в последовательности зацепления колес и не меняя размеров, указать, как надо установить колесо 2' на оси О2, чтобы вал О4 вращался в том же направлении, что и вал О1.
Задача 109. Определить передаточное отношение U16 и указать паразитные колеса ступенчатого редуктора. Исходные данные. Числа зубьев колес z1 = 20, z2 = 14, z3 = 40, z4 = 80, z5 = 20, z6 = 30.
|
|
|
|
|
|
§3 Проектирование планетарных редукторов
Многозвенные зубчатые механизмы с подвижными осями подразделяются на:
Ø планетарные редукторы и мультипликаторы – зубчатые механизмы с подвижной осью вращения, которые имеют опорное колесо и обладают одной степенью подвижности W = 1.
Ø дифференциальные механизмы – со степенью подвижности W = 2 или более, и которые не имеют опорного колеса.
Планетарные и дифференциальные механизмы изготавливают, как правило, соосными.
Рассмотрим структуру планетарного редуктора (рисунок 5.5, а).
|
|
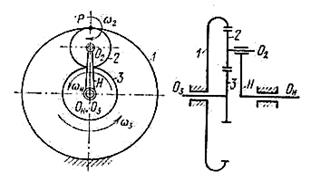
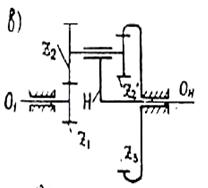
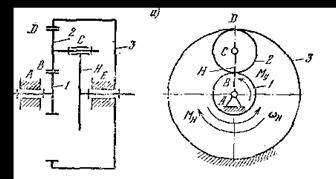
а - планетарный механизм; б - дифференциальный механизм.
Рисунок 5.5 - Механизмы с подвижными осями
Колеса с подвижными осями вращения называются планетарными или сателлитами (z2). Звено, на котором располагаются оси сателлитов называется водилом (на кинематических схемах водило обозначается буквой Н). Зубчатое колесо с неподвижной осью вращения называется солнечным или центральным (z1). Неподвижное колесо называется опорным (z3).
Проектирование планетарных редукторов заключается в подборе чисел зубьев при заданном передаточном отношении U31Н. При этом нужно учитывать, что сумма передаточных отношений в планетарном механизме при любых останавливаемых звеньях всегда равна 1
U31Н + UН13 = 1. (5.16)
В формуле (5.16) верхний индекс указывает индекс неподвижного звена. Тогда, U31Н - передаточное отношение 1-го колеса к водилу Н при неподвижном колесе 3; UН13 - передаточное отношение 1-го колеса к 3-му при неподвижном водиле Н.
Согласно формуле (5.16) передаточное отношение для планетарного редуктора (рисунок 5.5, а) примет вид
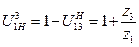, (5.17)
где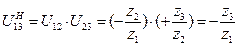 
.
Для дифференциального редуктора (рисунок 5.5, б)
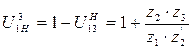, (5.18)
где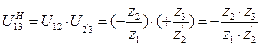 
.
При проектировании планетарных редукторов должны учитываться следующие условия:
Ø заданное передаточное отношение;
Ø заданный модуль m;
Ø отсутствие заклинивания колес передачи;
Ø числа зубьев должны быть целыми;
Ø числа зубьев z1 и z3 должны быть одинаковой четности;
Ø количество чисел зубьев 1-го колеса с внешним венцом должно быть не менее 17 (z1 ≥ 17);
Ø количество чисел зубьев 3-го колеса с внутренним венцом должно быть не менее 85 (z3 ≥ 85);
Ø колеса должны быть нулевыми (стандартными);
Ø условие соосности;
Ø условие соседства сателлитов;
Ø условие сборки.
Условие соосности необходимо, чтобы оси колес z1 и z3 располагались на одной оси, благодаря чему обеспечивается зацепление сателлитов с центральными колесами. Для планетарного редуктора с центральным колесом (рисунок 5.5, а) необходимо выполнение условия:
r1+2r2 = r3 или z1+ 2z2 = z3. (5.19)
Для дифференциального редуктора (рисунок 5.3, б) условие соосности имеет вид
z1+ z2 = z3 - z2¢. (5.20)
Для редуктора (рисунок 5.6) условие соосности имеет вид
z1+ z2 = z3 + z4. (5.21)
Условие соседства – условие совместного размещения нескольких сателлитов по общей окружности в одной плоскости. В редукторах для уменьшения нагрузок на зубья колес, с целью уменьшения габаритов, и из условий требований к динамической уравновешенности водила, устанавливают не один, а несколько сателлитов. Эти сателлиты располагаются под равными углами в одной плоскости и радиусы окружностей выступов сателлитов не должны пересекаться. При этом необходимо соблюдения следующего неравенства:
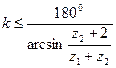. (5.22)
где k – число сателлитов.
Условие сборки (собираемости) – проверка условий соосности и соседства:
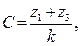(5.23)
где k – число теоретически возможных сателлитов, С - некоторое (целое!) число. Числа зубьев должны быть подобраны так, чтобы число сателлитов k получилось целым. Уравнения (5.22) и (5.23) нужно учитывать одновременно. Также необходимо, чтобы числа зубьев z1 и z3 имели одинаковую четность.
Примеры на определение передаточного отношения планетарного редуктора.
Пример 3.Рассчитать передаточное отношение U41Н планетарного редуктора (рисунок 5.6).
|
|
.
Пример 4.Рассчитать передаточное отношение U4Н1 планетарного редуктора (рисунок 5.6). Исходные данные взять из Примера 3.
Решение. Передаточное отношение от водила Н к колесу 1
.
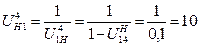Пример 5 на проектирование планетарного редуктора.Определить число зубьев 2-го колеса z2 и количество сателлитов k, если заданы числа зубьев z1=20, z3 = 70 (рисунок 5.5, а).
Решение. Из условия соосности (5.20) имеем
z2 = (z3 - z1)/2 = (70-20)/2 = 25.
По условию соседства (5.21), получаем
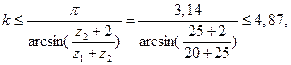
т.е. число сателлитов должно быть не более k ≤ 4. И, наконец, из условия сборки (5.22), имеем:
.
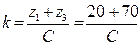Так как числа k и С должны быть целыми, то при выборе k = 4 условие (5.22) не может быть удовлетворено. Условию сборки удовлетворяет число сателлитов k = 3. Тогда С = 30.
Итак, z2 = 25 и k = 3.
Если задан модуль, можно также определить радиусы окружностей и межосевое расстояние (формулы (5.6)-(5.14)).
Дата добавления: 2015-06-01; просмотров: 7043;
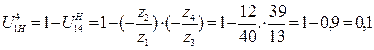