УРАВНЕНИЕ ДВИЖЕНИЯ МЕХАНИЗМА

После выполнения приведения сил и масс, любой механизм с одной степенью подвижности можно заменить его динамической моделью (рисунки 4.1; 4.5). Эта модель имеет переменный приведенный момент инерции I_пр и приведенный момент М_пр. Закон движения модели такой же, как и закон движения начального звена (уравнение 4.1).

Основой для составления уравнения движения механизма служит теорема об изменении кинетической энергии

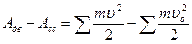, (4.8)

где υ – скорость в конце движения, υ_о – скорость в начале движения, А_дв – работа движущих сил, А_сс – работа сил сопротивления. При этом работу совершают все силы и моменты, а также силы трения.

Уравнение движения в энергетической форме. Если привести все силы и массы к звену приведения, то уравнение примет вид

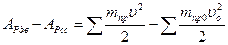, (4.9)

где А_Рдв – работа приведенной к звену приведения движущей силы, А_Рсс – работа приведенной силы сопротивления, m_пр и m_пр0 - приведенные массы, соответствующие конечному и начальному положениям.

Обычно удобнее в левую часть уравнения вводить работу приведенных моментов А_Мдв и М_Рсс, а правую часть выражать через приведенные моменты инерции I_пр и I_пр0. Тогда выражение (4.9) примет вид

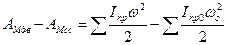. (4.10)

Уравнение движения в дифференциальной форме.Уравнение движения механизмов машинного агрегата запишем через приведенные силы и массы, для чего продифференцируем уравнение (4.9)

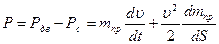, (4.11)

где Р_дв – движущая силы, Р_с – сила сопротивления.

То же самое уравнение можно записать, если воспользоваться приведенным моментом и приведенным моментом инерции, для чего продифференцируем уравнение (4.10)

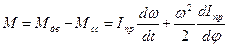. (4.12)

Уравнение движения в интегральной форме.В дифференциальное уравнение движения механизма машинного агрегата входят приведенные моменты движущих сил и сил сопротивления. Эти моменты могут быть функциями обобщенной координаты φ или ее первой производной φ' = ω, или времени t. Тогда уравнение (4.12) запишем в виде

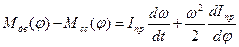. (4.13)

Интегрируя данное выражение по обобщенной координате, получим

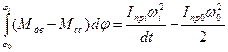. (4.14)