ТРЕНИЕ В КИНЕМАТИЧЕСКИХ ПАРАХ

В относительном движении соприкасающихся элементов кинематических пар, при наличии прижимающей их силы, между этими элементами возникает трение, на преодоление которого затрачивается работа двигателя, приводящего в движение механизм.

Кроме того, трение между элементами кинематических пар изменяет величину и направление реакции в этих парах. При скольжении элементов кинематических пар возникает сила трения скольжения F_тр, а при их перекатывании – момент трения перекатывания М_тр.

При исследовании физических факторов основ явления трения различают следующие виды трения:

· внешнее трение – сопротивление относительному перемещению, возникающее между двумя телами в зонах соприкосновения поверхностей и сопровождаемое диссипацией энергии;

· внутреннее трение – процессы, происходящие в твердых, жидких и газообразных телах при их деформации и приводящие к необратимому рассеянию механической энергии.

Сила трения – сила сопротивления при относительном перемещении одного тела по поверхности другого под действием внешней силы, тангенциально направленную к общей границе между этими телами.

В зависимости от состояния поверхностей трения различают

· сухое трение – трение без смазочного материала;

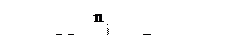жидкостное трение – трение со смазочным материалом.

В поступательной кинематической паре V класса (рисунок 3.16) реакция R₁₂ со стороны звена 1 (направляющая) на звено 2 (ползун) отклоняется от нормали n-n на угол трения φ в сторону, противоположную относительной скорости υ₂₁ звена 2 по отношению к звену 1.

Угол трения равен

φ=arctg f, (3.27)

где f – коэффициент трения скольжения.

Сила трения F_тр, приложенная к звену 2 со стороны звена 1, равна

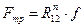, (3.28)

где 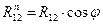- нормальная составляющая реакции R₁₂.

Если сила трения отсутствует, то .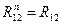

Во вращательной кинематической паре V класса (рисунок 3.17) линия действия реакции R₁₂ не будет проходить через центр О звена 2, а расположится по касательной к кругу трения с радиусом ρ. При этом момент трения М_тр направлен в противоположную сторону угловой скорости ω₂₁.

Радиус круга трения равен

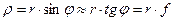, (3.29)

где r – радиус вала, f – коэффициент трения скольжения. Момент трения М_тр, который надо преодолеть для проворачивания вала 2 в подшипнике 1, будет равен

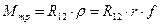. (3.30)

Если же трение отсутствует, то момент трения будет равен нулю (М_тр=0), а линия действия реакции R₁₂ пройдет через центр вала О.

В высшей кинематической паре IV класса (рисунок 3.18) реакция R₁₂ отклонится от нормали n-n на угол трения φ в сторону, противоположную направлению относительной скорости υ₂₁ точки А. Также к элементу пары приложен момент трения качения М_трк_., который направлен в сторону, противоположную направлению угловой скорости ω₂₁. Момент трения качения равен

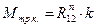, (3.31)

где k – коэффициент трения качения или плечо трения качения.

Рисунок 3.18. – Трение в высшей кинематической паре IV класса

На преодоление сил трения в кинематических парах затрачивается некоторая часть мощности двигателя, приводящего в движение механизм. Эта мощность N, затрачиваемая на преодоление трения в различных кинематических парах, подсчитывается следующим образом.

В поступательной паре V класса мощность рассчитывается

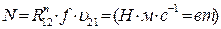, (3.32)

где υ₂₁ – скорость звена 2 по отношению к звену 1, равная алгебраической разности абсолютных скоростей звеньев 1 и 2

υ₂₁ = υ₂ - υ₁. (3.33)

Во вращательной паре V класса

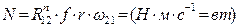, (3.34)

где ω₂₁ – угловая скорость звена 2 по отношению к звену 1, равная алгебраической разности абсолютных угловых скоростей звеньев 1 и 2

ω₂₁ = ω₂ - ω₁. (3.35)

В высшей паре IV класса мощность, затрачиваемая на преодоление трения скольжения, равна

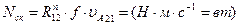, (3.36)

где f – коэффициент трения скольжения, υ_А21 – скорость точки А₂ звена 2 по отношению к точке А₁ звена 1.

Мощность, затрачиваемая на преодоление трения качения в этой же кинематической паре, равна

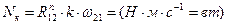, (3.37)

где k – коэффициент трения качения, ω₂₁ – угловая скорость звена 2 по отношению к звену 1.

Рассмотрим силовой расчет механизма, т.е. определение реакций в кинематических парах с учетом сил трения.

Пример. Для механизма шасси самолета (рисунок 3.19, а) найти мощность N, затрачиваемую на трение во всех кинематических парах. Исходные данные. Угловая скорость ω₁ = 0,3 сек^-1, положение первого звена φ₁ = 195⁰. Размеры звеньев: ℓ_АВ = 1,0 м, ℓ_AD = 1,32 м, ℓ_ВС = 0,4 м, ℓ_Е_D = 0,64 м, ℓ_С_D = 0,95 м, ℓ_ЕС = 0,3 м. К механизму приложены нагрузки: к звену 3 – сила тяжести G₃ = 100 H, приложена к центру масс S₃, расстояние до центра масс ℓ_DS₃ = 0,46 м, горизонтальная сила от набегающего воздушного потока Р = 400 Н, приложена к центру масс S₂, сила тяжести колеса G_К = 60 H, приложена к точке Е, звено 2 не нагружено. Диаметр цапф вращательных кинематических пар А, В, С, D соответственно равны d_A = 50 мм, d_B = 30 мм, d_C = 30 мм, d_D = 50 мм. Коэффициенты трения во всех кинематических парах f = 0,1.

Решение. 1). Строим схему механизма в масштабе μ_ℓ = 0,01 м/мм (рисунок 3.19, а).

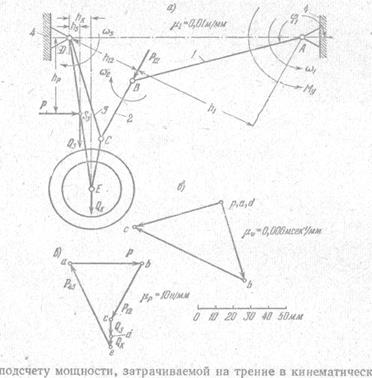
Рисунок 3.19 (63)

2). Строим план скоростей (рисунок 3.19, б) по уравнению

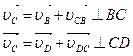
На плане скорость υ_В изображена отрезком 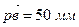, скорость υ_СВ - отрезком 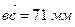, скорость υ_С - отрезком 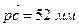. Масштаб плана скоростей

.

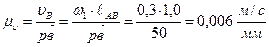3). Находим абсолютные угловые скорости звеньев (знак «плюс» приписываем скорости, направленной против движения часовой стрелки).

Угловая скорость ω₁ звена 1 известна (задана). Угловая скорость звена 2 равна

,

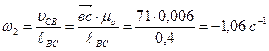а угловая скорость звена 3 равна

.

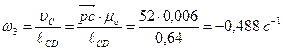4). Подсчитываем относительные угловые скорости по формуле (3.35)

ω₁₄ = ω₁ = 0,3 с^-1,

ω₁₂ = ω₁ - (-ω₁)= 0,3 + 1,06 = 1,36 с^-1,

ω₂₃ = -ω₃ - (-ω₂)= -0,488 + 1,06 = 0,572 с^-1.

5). Определяем реакции в кинематических парах.

а). Рассмотрим равновесие структурной группы 2-3 (II класса 1 вида). Звено 2 не нагружено, поэтому реакция R₁₂ в шарнире В направлена вдоль звена ВС. Эту реакцию находим из условия равновесия всей структурной группы. Для этого составляем сумму моментов всей структурной группы относительно точки D

,

где h_P, h₂, h₃, h₁₂ – плечи соответствующих сил, найденные по чертежу.

Величина реакции R₃₂в шарнире С равна R₃₂= -R₁₂, так звено 2 не нагружено. Реакцию R₄₃ в шарнире D определим из построения плана сил всей структурной группы

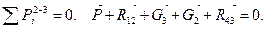
План сил строим в масштабе μ_Р=10 Н/мм (рисунок 3.19, в).

Соединяя начало силы Р с концом силы G₂ получаем вектор реакции R₄₃. На плане сил реакция R₄₃ изображается отрезком [еа] = 56 мм, поэтому

R₄₃ = [еа] · μ_Р = 56 · μ_Р = 560 Н.

б). Рассмотрим ведущее звено АВ. Составляем уравнение равновесия

,

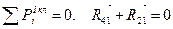но так как R₂₁ = - R₁₂, то R₄₁ = - R₁₂ =382 Н.

6). Рассчитываем мощность, теряемую на трение в кинематических парах, по формуле (3.34). Затрата мощности в каждой из пар А, В, С и D будет соответственно равна

,

,

,

.

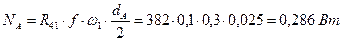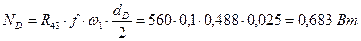Общая мощность N, теряемая на трение во всех парах, равна

Ответ. .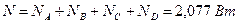

<24 25 262728 29 30 >

Дата добавления: 2015-06-01; просмотров: 4823;