ОПРЕДЕЛЕНИЯ УРАВНОВЕШИВАЮЩЕЙ СИЛЫ
В тех случаях, когда требуется найти только уравновешивающий момент Мур или уравновешивающую силу Рур, проще воспользоваться жестким рычагом Н.Е. Жуковского, не прибегая к последовательному силовому расчету всего механизма.
При равновесном состоянии механизма алгебраическая сумма мощностей внешних сил, приложенных к его звеньям, равна нулю. Эту сумму можно представить в следующем виде:
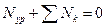, (3.21)
где Nур – мощность уравновешивающей силы,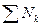 
- алгебраическая сумма мощностей остальных внешних сил, приложенных к k звеньям механизма, k – число нагруженных звеньев механизма.
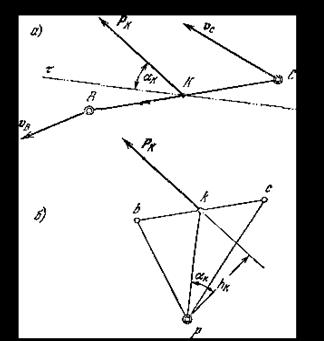
По Н.Е. Жуковскому, мощность любой силы можно найти следующим образом (рисунок 3.13, а).
|
|
Этот момент пропорционален мощности силы РК, что можно доказать следующим образом. Проводим через точку К прямую τ-τ, перпендикулярную направлению вектора скорости точки К на повернутом плане скоростей. Очевидно, что прямая τ-τ имеет направление касательной к траектории точки К.
Запишем выражение для мощности силы РК
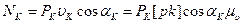, (3.23)
где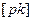 
- отрезок на плане скоростей, 
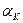- угол между направлением скорости 
точки К и направлением силы РК, 
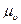- масштаб плана скоростей.
Теперь замечаем, что угол 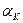равен углу между вектором 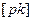на плане скоростей и плечом hK. Поэтому 
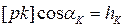и выражение (3.23) перепишется так
. (3.24)
Правые части формул (3.22) и (3.24) отличаются только множителем 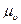, который будет общим при выражении мощности любой силы, приложенной к механизму, по формуле (3.24) (поскольку используется один и тот же план скоростей).
Это позволяет формулу (3.21) записать в другой форме
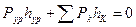, (3.25)
откуда
. (3.26)
Следовательно, если задан механизм и все внешние силы, приложенные к нему, то для нахождения уравновешивающей силы можно поступать следующим образом
1. построить повернутый план скоростей механизма,
2. найти на этом плане по правилу подобия точки приложения заданных внешних сил,
3. в одноименные точки плана перенести параллельно самим себе силы с механизма, включая и уравновешивающую силу,
4. принять повернутый скоростей за рычаг с точкой опоры в полюсе р, написать уравнение равновесия этого рычага по формуле (3.25) и из него найти величину уравновешивающей силы Рур по формуле (3.26).
Необходимо указать, что если к звеньям механизма приложен внешний момент, то его следует представить в виде пары сил, которые и надо переносить в соответствующие точки повернутого плана скоростей. Рычагом Жуковского непосредственно находится уравновешивающая сила. Уравновешивающий момент определяется умножением уравновешивающей силы на её плечо относительно оси звена, к которому она приложена (формула (3.22)).
Дата добавления: 2015-06-01; просмотров: 1709;