ОПРЕДЕЛЕНИЕ СИЛ ИНЕРЦИИ В МЕХАНИЗМАХ

Силы инерции материальных точек звена могут быть приведены к одной точке и, таким образом, представлены их главным вектором и главным моментом.

Главный вектор сил инерции, называемый обычно силой инерции звена, равен

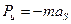. (3.1)

где m[кг] – масса звена, a_S[мсек^-2] – ускорение центра S масс звена. Направление силы инерции P_и противоположно по направлению вектора a_S. Её размерность [кгмсек^-2], т.е. она измеряется в ньютонах [Н].

Мы ограничимся рассмотрением случаев, когда звено совершает плоскопараллельное движение и имеет плоскость материальной симметрии, параллельную плоскости его движения. При этом точкой приведения сил инерции звена целесообразно брать его центр масс (рисунок 3.1), так как упрощается выражение момента инерционной пары сил – главного момента сил инерции, что то же, инерционного момента. Он оказывается равным

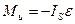, (3.2)

где I_S [кгм²] – момент инерции масс звена относительно оси, проходящей через его центр масс перпендикулярно плоскости его материальной симметрии, или, иначе, центральный момент инерции звена, ε [сек^-2] - угловое ускорение звена.

Инерционный момент М_и имеет размерность [кгмсек^-2]=[Нм]. Плоскость, в которой он действует, параллельна плоскости движения звена; он направлен в сторону, противоположную направлению углового ускорения звена (рисунок 3.1).

Частные случаи инерционной нагрузки

· Поступательное движение звена (рисунок 3.2, а). Инерционная нагрузка состоит из одной инерционной силы Р_и, определяемой формулой (3.1).

· Неравномерное вращательное движение звена (рисунок 3.2, б). Инерционная нагрузка состоит из силы инерции Р_и, определяемой формулой (3.1), и инерционного момента М_и, определяемого формулой (3.2). Модуль полного ускорения центра масс звена в этом случае равен

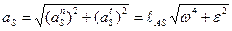, (3.3)

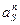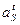где и - нормальное (центростремительное ) и касательное (тангенциальное) ускорения центра масс звена, ω и ε – угловая скорость и угловое ускорение звена, ℓ_AS – расстояние от центра масс S до оси А вращения звена.

Силу Р_и и момент М_и можно привести к одной силе .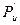

Для этого следует силу Р_и приложить, сохраняя ее направление, в центре К качания звена (рисунок 3.2, в). Расстояние ℓ_AK центра качания К звена от оси вращения последнего А равно

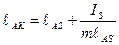, (3.4)

где I_S – центральный момент инерции звена, а m – его масса.

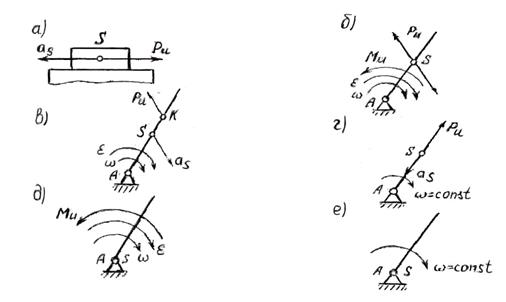
Рисунок 3.2 – Частные случаи инерционной нагрузки

· Равномерное вращательное движение звена (рисунок 3.2, г). Инерционная нагрузка состоит только из силы инерции Р_и звена, которая в этом случае направлена по линии AS противоположно направлению вектора центростремительного (нормального) ускорения центра масс звена. Это ускорение равно

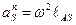, (3.5)

и, следовательно, центробежная сила инерции будет рана

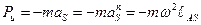. (3.6)

Произведение mℓ_AS называется неуравновешенностью или дисбалансом и имеет размерность [кг·м].

· Неравномерное вращательное движение звена при совпадении центра масс S звена с его осью вращения А (рисунок 3.2, д). В этом случае инерционная нагрузка звена состоит только из инерционного момента М_и, который находится по формуле (3.2).

· Равномерное вращательное движение звена при совпадении центра масс S звена с его центром вращения А (рис. 3.2, е). В этом случае ℓ_AS = 0 и в соответствии с формулой (3.3) a_S=0, следовательно, Р_и=0, и так как ε=0 (равномерное вращение), то М_и=0.

В этом случае инерционная нагрузка звена равна нулю и оно называется уравновешенным (следует помнить, что рассматривается плоская система сил).

Пример. Для кривошипно-ползунного механизма (рисунок 3.3) определить инерционную нагрузку всех звеньев.

Исходные данные: длины звеньев ℓ_АВ=0,074 м, ℓ_ВС=0,200 м; положения центров масс ℓ_АS1=0,020 м, ℓ_ВS2=0,060 м; массы звеньев m₁=10 кг, m₂=0,5 кг, m₃=0,4 кг; осевой момент инерции шатуна I_S2=0,0018 кгм²; угловая скорость кривошипа ω₁=200 с^-1.

Задачу решить для положения, когда угол φ=45^о.

Решение. 1). Построение схемы механизма (рисунок 3.3, а).

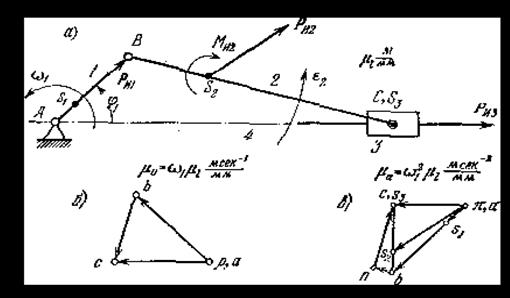
Рисунок 3.3 – Определение инерционной нагрузки звеньев

кривошипно-ползунного механизма

Задаемся масштабом чертежа μ_ℓ=0,001 м/мм и строим схему механизма. Чертежные длины звеньев определятся

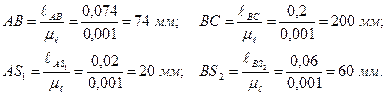
2). Построение плана скоростей(рисунок 3.3,б). Рассчитываем масштаб скорости в масштабе кривошипа.μ_υ = ω₁ μ_ℓ=200·0,001= 0,20 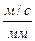. Тогда длина вектора скорости υ_В, т.е. отрезок (Рb), будет равен (АВ)=(Рb)=74 мм. Точку “с” на плане скоростей находим по векторному уравнению

.

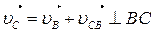3). Построение плана ускорений(рисунок 3.3, в). Строим план ускорений в масштабе кривошипа

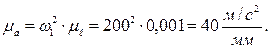
Тогда на плане ускорений отрезок (πb), изображающий вектор нормального ускорения точки В, будет равен (АВ)=(πb)=74 мм. Точку “с” находим по векторному уравнению

.

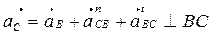Отрезок (nb), изображающий на плане нормальное ускорение 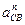, определится из равенства

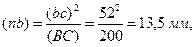
где (bс)=52 мм – отрезок, замеренный с плана скоростей.

ТочкиS₁, S₂определим по правилу подобия, п.2. Но т.к. план ускорений построен в масштабе кривошипа, то (πs₁)=(AS₁)= 20 мм, (bs₂)=(BS₂)= 60 мм. Тогда ускорения центров масс определятся

a_S1 = (πs₁)·μ_a = 20·40 = 800 м/с²,

a_S2 = (πs₂)·μ_a = 64·40 = 2560 м/с²,

a_S3 = а_С =(πс)·μ_a = 56·40 = 2240 м/с².

Угловые ускорения находятся по формулам

ε₁=0, т.к. ω₁=const,

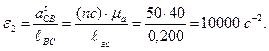
Направление ε₂ будет против часовой стрелки в соответствие с направлением 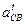тангенциального ускорения точки С звена ВС относительно точки В (рисунок 3.3, а).

4). Расчет инерционной нагрузкидля каждого звена.

а)Расчет инерционных сил.Сила инерции кривошипа равна

Р_и1=m₁a_S1=10·800=8000 H.

Вектор силы инерции приложен к центру масс кривошипа и направлен в противоположную сторону вектору ускорения a_S1.

Сила инерции шатуна

Р_и2=m₂a_S2=0,5·2560=1280 H.

Вектор силы инерции приложен к центру масс шатуна и направлен в противоположную сторону вектору ускорения a_S2.

Сила инерции ползуна

Р_и3=m₃a_С=0,4·2240=896 H.

Вектор силы инерции приложен к центру масс ползуна и направлен в противоположную сторону вектору ускорения a_С.

б)Расчет инерционных моментов. Для кривошипа инерционный момент равен М_и1=0, т.к. звено вращается равномерно.

Для шатуна инерционный момент определится по формуле

М_и2= ε₂·I_S2=10000·0,0018=18 Нм.

Этот момент направлен в противоположную сторону угловому ускорению.

Для ползуна момент инерции М_и3=0, т.к. звено движется поступательно.