ЗАДАЧИ 48-51

Задача 48. Определить массу противовеса m_пр, который надо установить на вращающийся вал для уравновешивания сил инерции грузов с массами m₁, m₂, m₃ и m₄, лежащих в одной перпендикулярной к оси вала плоскости. Исходные данные: координата центра масс S_пр противовеса ρ_пр=15 мм; массы грузов m₁=5 кг, m₂=7 кг, m₃=8 кг, m₄=10 кг; расстояния от оси вала до центров масс S₁, S₂, S₃ и S₄ грузов равны ρ₁=10 мм, ρ₂=20 мм, ρ₃=14 мм, ρ₄=10 мм; углы закрепления грузов α₁₂=α₂₃=α₃₄=90^о.

Задача 49. Определить массы противовесов m_пр1 и m_пр2, которые надо установить на плоскости уравновешивания I и II для уравновешивания сил инерции грузов с массами m₁, m₂, m₃ и m₄, лежащих в плоскости, содержащей ось вала. Исходные данные: координаты центров масс S_пр1 и S_пр2 противовесов ρ_пр1=50 мм, ρ_пр2=40 мм; массы грузов m₁=2 кг, m₂=3 кг, m₃=2 кг, m₄=4 кг; расстояния от оси вала до центров масс S₁, S₂, S₃ и S₄ грузов равны ρ₁=10 мм, ρ₂=16 мм, ρ₃=12 мм, ρ₄=20 мм; расстояния между грузами ℓ₁₂=ℓ₂₃=ℓ₃₄=100 мм.

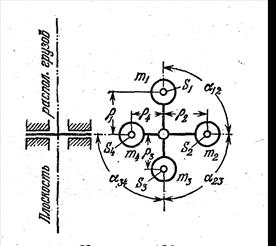
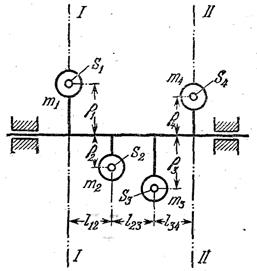
К задаче 48 К задаче 49

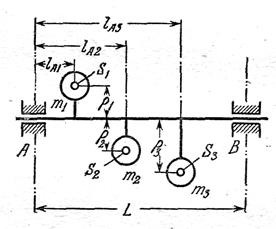
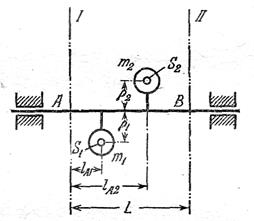
К задаче 50 К задаче 51

Задача 50. Определить реакции R_A и R_B в подшипниках вала от сил инерции грузов. Исходные данные: массы грузов m₁=1,0 кг, m₂=0,5 кг, m₃=0,25 кг; центры масс всех грузов расположены в плоскости, содержащей ось вращения вала АВ. Координаты центров масс S₁, S₂, иS₃ грузов равны ρ₁=100 мм, ρ₂=100 мм, ρ₃=200 мм; расстояния грузов от подшипника А: ℓ_А1=100 мм, ℓ_А2=300 мм, ℓ_А3=400 мм; расстояния между опорами А и В L=500 мм, угловая скорость вала ω=20 с^-1.

Задача 51. Определить массы противовесов m_пр1 и m_пр2, которые надо установить на плоскости уравновешивания I и II для уравновешивания сил инерции грузов с массами m₁ иm₂, лежащих в плоскости, содержащей ось вращения вала. Исходные данные: координаты центров масс S_пр1 и S_пр2 противовесов ρ_пр1=ρ_пр2=100 мм; массы грузов m₁=0,2 кг, m₂=0,1 кг; координаты центров масс S₁ и S₂ грузов от плоскости уравновешивания I равны ℓ_А1=200 мм, ℓ_А2=400 мм; расстояния между плоскостями уравновешивания L=600 мм.

3.2.2 Полное или частичное уравновешивание результирующей силы инерции механизма.Для решения этой группы задач необходимо построить схему механизма, одна из точек которого описывает траекторию движения общего центра масс механизма. Затем построить планы скоростей и ускорений и определить главный вектор сил инерции по формуле

Р_и=-m_∑ а_S, (3.8)

где m_∑ - суммарная масса всех подвижных звеньев механизма, а_S – ускорение общего центра масс механизма.

Главный вектор Р_исил инерции механизма будет равен нулю только тогда, когда вектор полного ускорения а_S центра масс будет также равен нулю. Это условие выполняется, если общий центр масс S механизма находится в точке, неподвижной относительно стойки. При частичном уравновешивании вектора Р_и он может иметь заданное направление или модуль.

§1 Определение общего центра масс механизма.Положение центра масс механизма может быть найдено методом главных векторов из условия, что

r_S=∑h_i, (3.9)

где r_S – радиус-вектор общего центра масс механизма, h_i – главный вектор силы инерции i-того звена.

Применительно к шарнирному четырехзвенному механизму (рисунок 3.5) и кривошипно-ползунному механизму (рисунок 3.6) соотношение (3.9) примет вид

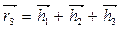, (3.10)

где r_S – радиус-вектор общего центра масс механизма, h₁ – главный вектор силы инерции кривошипа ОА, h₂ – главный вектор силы инерции шатуна АВ, h₃ – главный вектор силы инерции коромысла ВСили ползуна. Все эти вектора параллельны звеньям, т.е.

h₁÷÷ ℓ_ОА, h₂÷÷ ℓ_АВ, h₃÷÷ ℓ_ВС.

Величины главных векторов сил инерции звеньев равны

h₁= [m₁ℓ_OS1+(m₂+m₃)ℓ_ОА]/m_∑

h₂=[m₂ℓ_АS2+(m₃)ℓ_АВ]/m_∑ (3.11)

h₃=m₃ℓ_BS3/m_∑,

где m₁, m₂, m₃ - массы звеньев (кг); суммарная масса m_∑ = m₁ + m₂ + m₃, ℓ_OS1, ℓ_АS2, ℓ_BS3 – расстояния до центров масс звеньев (м); ℓ_ОА, ℓ_АВ, ℓ_ВС – длины звеньев (м).

Как видно из соотношений (3.11), модули векторов h₁, h₂, h₃ зависят от величин и расположения масс подвижных звеньев.

Рассмотрим определение общего центра масс каждого механизма.

Пример 1. Определить общий центр масс коромыслового механизма(рисунок 3.5).Исходные данные. Длины звеньев в м: ℓ_ОА, ℓ_АВ, ℓ_ВС; расстояния до центров масс в м: ℓ_ОS1, ℓ_АS2, ℓ_ВS3; массы звеньев в кг: m₁, m₂, m₃. Массы звеньев сосредоточены в центрах масс.

Определить. r_S - радиус-вектор, определяющий положение центра тяжести механизма.

Решение. Рассчитываем масштабный коэффициент длины μ_ℓ = ℓ_ОА/ОА и изображаем схему механизма (см. главу 2, §2.1, 2.2, 2.3).

По формулам (3.11) определим величины главных векторов сил инерции

h₁= [m₁ℓ_OS1+(m₂+m₃)ℓ_ОА]/m_∑

h₂=[m₂ℓ_АS2+(m₃)ℓ_АВ]/m_∑

h₃=m₃ℓ_BS3/m_∑,

где m_∑ = m₁ + m₂ + m₃.

Рассчитаем чертежные величины главных векторов сил инерции

[h₁]=h₁/μ_ℓ; [h₂]=h₂/μ_ℓ; [h₃]=h₃/μ_ℓ.

Радиус-вектор положения центра масс определяется по формуле (3.10):

.

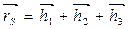Уравнение векторное, поэтому решаем его, применяя правила сложения векторов. Из точки О на схеме механизма (рисунок 4.4) проводим вектор h₁÷÷ℓ_ОА длиной [h₁]. К концу этого вектора прибавляем вектор h₂÷÷ℓ_АВ длиной [h₂], а затем вектор h₃÷÷ℓ_ВС длиной [h₃]. Конец вектора h₃ даст точку S – центр масс механизма. Соединим точкуS с точкой О – получим чертежное значение вектора r_S.

Рисунок 3.5. - Определение центра масс коромыслового механизма

Действительное значение радиус-вектора положения центра масс определиться по формуле:

r_S = [r_S]μ_ℓ = (м),

где [r_S] - чертежное значение радиус-вектора, замеренное с чертежа в мм.

Пример 2. Определить общий центр масс кривошипно-ползунного механизма(рисунок 3.6). Исходные данные. Длины звеньев в м: ℓ_ОА, ℓ_АВ; расстояния до центров масс в м: ℓ_ОS1, ℓ_АS2, ℓ_ВS3; массы звеньев в кг: m₁, m₂, m₃. Массы звеньев сосредоточены в центрах масс.

Определить. r_S - радиус-вектор, определяющий положение центра тяжести механизма.

Решение. Аналогично предыдущему Примеру 1 вычисляем масштабный коэффициент длины μ_ℓ и вычерчиваем схему механизма (рисунок 3.6). Вычисляем главные вектора сил инерции по формулам (3.11):

h₁= [m₁ℓ_OS1+(m₂+m₃)ℓ_ОА]/m_∑

h₂=[m₂ℓ_АS2+(m₃)ℓ_АВ]/m_∑

h₃=m₃ℓ_BS3/m_∑,

где m_∑ = m₁ + m₂ + m₃.

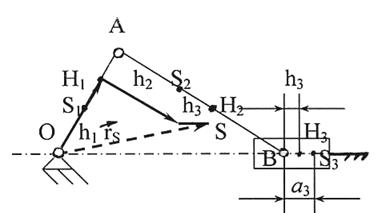
Рисунок 3.6. - Определение центра масс кривошипно-ползунного

механизма

Вычисляем чертежные значения главных векторов сил инерции: [h₁]=h₁/μ_ℓ, [h₂]=h₂/μ_ℓ, [h₃]=h₃/μ_ℓ. Внимание! Если центр масс S₃ ползуна совпадает с точкой В, то а₃=0 и h₃=0. Радиус-вектор общего центра масс определиться из векторного уравнения (3.10)

.

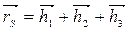Из построения определиться чертежное значение r_S, а по формуле r_S = [r_S]μ_ℓ, действительное значение радиус-вектора в м.