Полное уравновешивание результирующей силы инерции.

Для полного уравновешивания главного вектора сил инерции и главного момента сил инерции необходимо, чтобы радиус-вектор положения общего центра масс механизма был равен нулю:

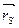= 0. (3.15)

В этом случае центр масс механизма должен совпадать с точкой О. Эти условия должны соблюдаться в том случае, если главные вектора сил инерции также равны нулю:

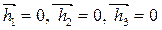Откуда имеем:

m₁ℓ_О_S₁=-(m₂+m₃)ℓ_ОА,

m₂ℓ_А_S₂=-(m₃)ℓ_АВ, (3.16)

m₃ℓ_В_S₃=0.

Уравнения (3.16) являются условием полного уравновешивания результирующей силы инерции. Из этих уравнений видно, что, так как расстояния ℓ_О_S₁ и ℓ_А_S₂отрицательны, то противовесы устанавливаются в противоположные стороны от центров масс звеньев. Для полного уравновешивания шарнирного четырехзвенника необходимо установить три противовеса, а для уравновешивания кривошипно-ползунногомеханизма – два.

Пример 5. Полное уравновешивание кривошипно-ползунного механизма(рисунок 3.9). Исходные данные. Длины звеньев в м: ℓ_ОА=0,3; ℓ_АВ=0,7; расстояния до центров масс в м: ℓ_OS₁=0,2; ℓ_AS₂=0,35; ℓ_В_S₃=0; расстояние до центров масс противовесов ℓ΄_OS₁=0,1; ℓ΄_А_S₂=0,2; массы звеньев в кг: m₁=3; m₂=6, m₃=8.

Определить: m_пр1, m_пр2 (кг) – массы противовесов, необходимые для полного уравновешивания главного вектора сил инерции.

Решение. Известно, что для полного уравновешивания кривошипно-ползунного механизма необходимо установить два противовеса, которые будут располагаться в противоположную сторону от центров масс S₁ и S₂ (рисунок 3.9).

Главный вектор результирующей силы инерции будет полностью уравновешен, если удовлетворяются условия (3.15) и (3.16), т.е.:

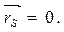
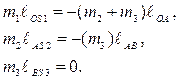
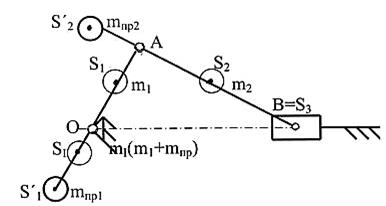
Рисунок 3.9. - Полное уравновешивание кривошипно-ползунного механизма

Так как необходимо установить два противовеса, то третье уравнение системы не учитываем.

Рассмотрим 2-е звено. После установки противовеса масса звена станет

m_II = m₂+ m_пр2.

Центр масс сместится и встанет в точку S₂.

Тогда 2-ое уравнение системы (3.16) примет вид

m_II ℓ_А_SII =-(m₃)ℓ_АВ.

Составим уравнение статического момента 2-го звена относительно точки A:

m_IIℓ_А_SII = m₂ℓ_А_S₂- m_пр2ℓ_А_S΄₂.

Приравнивая оба эти равенства, определим массу 2-го противовеса:

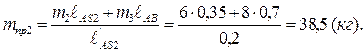
Тогда полная масса 2-го звена

m_II = m₂+ m_пр2 = 6 + 38,5 =44,5 кг.

Рассмотрим 1-ое звено. После установки противовеса центр масс 1-го звена сместится и встанет в точку S_I. Масса звена изменится и станет равной

m_I = m₁+ m_пр1.

1-ое уравнение из условия (3.16) запишется следующим образом

m_Iℓ_OSI = -(m_II + m₃)ℓ_ОА.

Составим уравнение статического момента 1-го звена относительно точки О:

m_Iℓ_OSI = m₁ℓ_OS₁- m_пр1ℓ_OS΄₁.

Приравнивая оба эти равенства, определим массу 1-го противовеса:

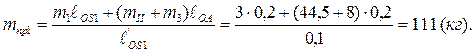
Пример 6. Полное уравновешивание коромыслового механизма(рисунок 3.10). Исходные данные. Длины звеньев в м: ℓ_ОА=0,3; ℓ_АВ=0,7; ℓ_ВС=0,6; расстояния до центров масс в м: ℓ_OS₁=0,2, ℓ_AS₂=0,35, ℓ_В_S₃=0,3; массы звеньев в кг: m₁=3; m₂=6; m₃=8; расстояния до центров масс противовесов в м: ℓ΄_OS₁=0,1; ℓ΄_А_S₂=0,2; ℓ΄_В_S₃=0,2.

Определить массы противовесов в кг: m_пр1, m_пр2, m_пр3, необходимые для полного уравновешивания главного вектора сил инерции шарнирного четырехзвенника. Решение. Механизм будет полностью уравновешен, если выполняются условия (3.15) и (3.16), т.е.:

S^΄₃

m_пр3

S^΄₂ S_II S₂ В

m_пр2 А m₂ S_III m_III(m₃₊m_пр3)

S₁ m_II(m₂+m_пр₂)

S_I m₁ S₃m₃

m_I(m₁+m_пр1)

О С

S^΄₁

m_пр1

Рисунок 3.10. – Полное уравновешивание коромыслового механизма

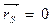; (3.15)

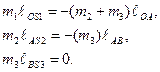(3.16)

Рассмотрим 3-е звено. После установки противовеса масса звена изменится и станет

m_III = m₃+ m_пр3.

Центр масс сместится в точку S_III. Расстояние до центра масс станет ℓ_В_SIII. Из третьего уравнения системы (3.16), имеем m_IIIа_III = 0. Но m_III ¹ 0.

Поэтому условие (3.16) не выполняется. Массу противовеса m_пр3 определим, составив уравнение статического момента 3-его звена относительно точки В:

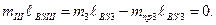
Выразим массу противовеса:

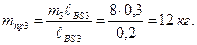
Тогда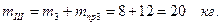

Рассмотрим 2-ое звено. Масса звена после установки противовеса m_II=m₂+m_пр2. Расстояние до центра масс а_II =ℓ_А_SII. Из второго уравнения системы (3.16) имеем:

m_IIℓ_А_S_II= -(m_III)ℓ_АВ.

Составим уравнение статического момента 2-го звена относительно точки А:

m_IIℓ_А_SII = m₂ℓ_А_S₂- m_пр2ℓ_А_S΄₂.

Приравнивая правые части обоих уравнений и выразив m_пр2, получим:

m_пр2=(m₂ℓ_А_S₂+m_IIIℓ_АВ)/ ℓ_А_S΄₂=(кг).

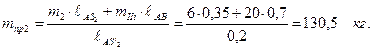
Тогда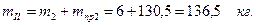

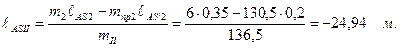
Рассмотрим 1-ое звено. Масса звена после установки противовеса m_I = m₁+m_пр1. Расстояние до центра масс ℓ_О_SI. Из первого уравнения системы (3.16) имеем:

m_Iℓ_OSI = - (m_II + m_III)ℓ_ОА.

Составим уравнение статического момента 1-го звена относительно точки О:

m_Iℓ_OSI = m₁ℓ_OS₁-m_пр1ℓ_OS΄₁.

Приравнивая правые части обоих уравнений и выразив m_пр1, получим:

<15 16 171819 20 21 >

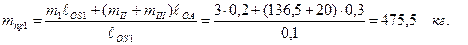
Дата добавления: 2015-06-01; просмотров: 1553;