Частичное уравновешивание результирующей силы инерции.

Частичное уравновешивание применяется для уравновешивания только главного вектора сил инерции без уравновешивания моментов сил инерции. При этом необходимо и достаточно, чтобы общий центр масс S механизма оставался неподвижным, т.е. находился между точками О и С, и удовлетворялось условие

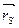=const. (3.12)

Как было указано выше, радиус-вектор положения общего центра масс r_S определяется как геометрическая сумма главных векторов сил инерции

Для удовлетворения условия (3.12) нужно, чтобы

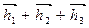= const. (3.13)

В результате этого имеем:

m₁ℓ_О_S₁=[-m₂ℓ_ОА(ℓ_АВ-ℓ_AS₂)]/ℓ_АВ

m₂ℓ_AS₂=[-m₃ℓ_ВС(ℓ_ВС-ℓ_В_S₃)]/ℓ_АВ. (3.14)

Уравнения (3.14) являются условием частичного уравновешивания механизма. Из выражений (3.14) следует, что частичное уравновешивание шарнирного четырехзвенника может быть достигнутопутем установки противовесов на двух его звеньях. Частичное же уравновешивание кривошипно-ползунного механизма достигается установкой одного противовеса.Знак «минус» показывает, что противовес должен быть установлен вне звена (рисунки 3.7 и 3.8).

Пример 3. Частичное уравновешивание кривошипно-ползунного механизма (рисунок 3.7). Исходные данные. Длины звеньев в м: ℓ_ОА= 0,1, ℓ_АВ= 0,4; расстояния до центров масс в м: ℓ_OS₁= 0,075, ℓ_AS₂= 0,15, ℓ_В_S₃=0; расстояние до центра масс 1-го противовеса ℓ΄_OS₁= 0,2 м; массы звеньев в кг: m₁= 0,3; m₂= 1,5; m₃= 2,0.

Определить: m_пр (кг) – массу противовеса, необходимую для частичного уравновешивания главного вектора сил инерции.

Решение. Известно, что для частичного уравновешивания кривошипно-ползунного механизма достаточно установить один противовес, который будет располагаться в противоположную сторону от центра масс S₁ (рисунок 3.7).

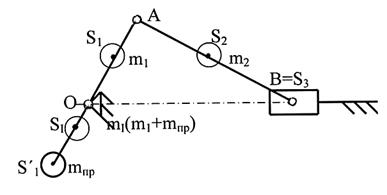
Рисунок 3.7. - Частичное уравновешивание

кривошипно-ползунного механизма

Главный вектор результирующей силы инерции будет частично уравновешен, если удовлетворяются условие

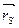= const.

Так как необходимо установить один противовес, то достаточно рассмотреть первое уравнение из выражения (3.14):

m₁ℓ_О_S₁=[-m₂ℓ_ОА(ℓ_АВ-ℓ_AS₂)]/ℓ_АВ.

Рассмотрим 1-ое звено. После установки противовеса центр масс 1-го звена сместится и встанет в точку S_I. Масса звена изменится и станет равной

m_I = m₁+ m_пр1.

1-ое уравнение из условия (3.14) запишется следующим образом

m_Iℓ_О_SI = [-m₂ℓ_ОА(ℓ_АВ-ℓ_AS₂)]/ℓ_АВ.

Составим уравнение статического момента 1-го звена относительно точки О:

m_Iℓ_О_SI = m₁ℓ_О_S₁- m_пр1ℓ_О_S΄₁

Приравнивая оба эти равенства, определим массу противовеса:

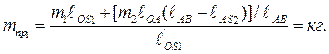
После подстановки имеем

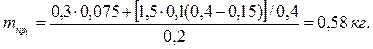
Пример 4. Частичное уравновешивание коромыслового механизма(рисунок 3.8). Исходные данные. Длины звеньев в м: ℓ_ОА = 0,3 м, ℓ_АВ = 0,6 м, ℓ_ВС = 0,5 м; расстояния до центров масс в м: ℓ_OS₁ = 0,2 м, ℓ_AS₂ = 0,25 м, ℓ_В_S₃ = 0,2 м; массы звеньев в кг: m₁ = 5, m₂ = 7, m₃ = 9; расстояния до центров масс противовесов ℓ΄_OS₁ = 0,15 м, ℓ΄_А_S₂ = 0,3 м.

Определить массы противовесов m_пр1, m_пр2в кг, необходимые для частичного уравновешивания главного вектора сил инерции шарнирного четырехзвенника.

Решение. Механизм будет частично уравновешен, если выполняются условия (3.98), (3.100) и (3.101).

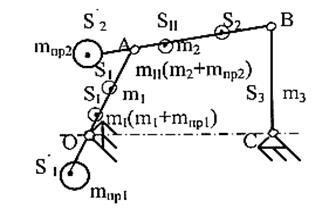
Рисунок 3.8. - Частичное уравновешивание шарнирного

четырехзвенника

Рассмотрим 2-е звено. После установки противовеса масса звена изменится и станет

m_II = m₂+ m_пр2.

Центр масс сместится в точку S_II. Расстояние до центра масс станет а_II=ℓ_А_SII. Из второго уравнения системы (3.101), имеем

m₂ℓ_AS₂=[-m₃ℓ_ВС(ℓ_ВС-ℓ_В_S₃)]/ℓ_АВ.

Преобразуем его с учетом установки противовеса

m_IIℓ_А_SII=[-m₃ℓ_ВС(ℓ_Вс-ℓ_В_S₃)]/ℓ_АВ.

Составим уравнение статического момента 2-го звена относительно точки А:

m_IIℓ_А_SII = m₂ℓ_А_S₂- m_пр2ℓ_А_S΄₂.

Приравнивая правые части обоих уравнений и выразив m_пр2, получим:

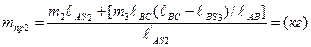После подстановки имеем

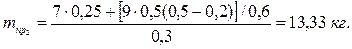
Тогда полная масса 2-го звена

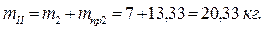
ℓ_ОА = 0,3 м, ℓ_АВ = 0,6 м, ℓ_ВС = 0,5 м; расстояния до центров масс в м: ℓ_OS₁ = 0,2 м, ℓ_AS₂ = 0,25 м, ℓ_В_S₃ = 0,2 м; массы звеньев в кг: m₁ = 5, m₂ = 7, m₃ = 9; расстояния до центров масс противовесов ℓ΄_OS₁ = 0,15 м, ℓ΄_А_S₂ = 0,3 м.

Определим расстояние до смещенного центра масс

m_IIℓ_А_SII = m₂ℓ_А_S₂- m_пр2ℓ_А_S΄₂.

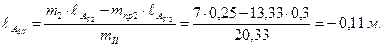
Знак «минус» показывает, что центр масс сместился влево от точки А. При дальнейших расчетах его учитывать не надо!

Аналогично рассмотрим 1-ое звено. Масса звена после установки противовеса m_I = m₁+m_пр1. Расстояние до центра масс а_I = ℓ_О_SI. Из первого уравнения системы (3.101) имеем:

m_Iℓ_О_SI=[-m_IIℓ_ОА(ℓ_АВ-ℓ_А_SII)]/ℓ_АВ.

Составим уравнение статического момента 1-го звена относительно точки О:

m_Iℓ_О_SI = m₁ℓ_О_S₁-m_пр1ℓ_О_S΄₁.

Приравнивая правые части обоих уравнений и выразив m_пр1, получим:

<14 15 161718 19 20 >

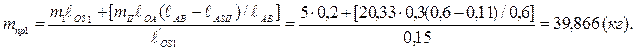
Дата добавления: 2015-06-01; просмотров: 1433;