Прямой метод Ляпунова
Наиболее общие результаты по исследованию устойчивости нелинейных систем могут быть получены по методу А.М. Ляпунова.
При использовании прямого метода Ляпунова, именуемого также второй методой Ляпунова, исследуемая система описывается дифференциальными уравнениями в форме уравнений первого порядка, полагая, что они записаны для переходного процесса в отклонениях всех переменных xi (i = 1, 2, ... , n) от их значений в установившемся процессе при новых постоянных значениях возмущающего f = f0 и задающего g = g0 воздействий. Следовательно, эти уравнения для нелинейной системы n-го порядка будут:
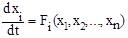 при i = 1, 2, ... , n, (2.1)
при i = 1, 2, ... , n, (2.1)
где Fi - нелинейные функции произвольного вида, удовлетворяющие условию
F1 = F2 = ... = Fn = 0 при x1 = x2 = ... = xn = 0, (2.2)
так как в установившемся состоянии все отклонения и их производные равны нулю.
Чтобы исследовать устойчивость по Ляпунову, необходимо подобрать некоторую знакоопределенную функцию V и вычислить производную по времени от этой функции.
Функция V называется знакоопределенной в некоторой области, если она во всех точках этой области в окрестности начала координат сохраняет один и тот же знак и нигде не обращается в нуль, кроме начала координат.
Функция V называется знакопостоянной, если она сохраняет один и тот же знак, но может обращаться в нуль не только в начале координат, но и в других точках данной области.
Функция V называется знакопеременной, если она в данной области вокруг начала координат может иметь разные знаки.
Функция Ляпунова и ее производная по времени. Любая функция
V = V(x1, x2, ..., xn ), (2.3)
тождественно обращающаяся в нуль при x1 = x2 = ... = xn = 0, называется функцией Ляпунова, если в ней в качестве x1, x2, ..., xn взяты переменные, в которых записаны уравнения (2.1) для этой системы.
Производная от функции Ляпунова (2.3) по времени будет
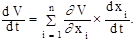 (2.4)
(2.4)
Подставив значения 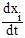 (i = 1, 2, ... , n) из уравнений системы (2.1), получим
(i = 1, 2, ... , n) из уравнений системы (2.1), получим
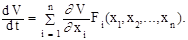 (2.5)
(2.5)
Следовательно, производная от функции Ляпунова по времени, так же как и сама V, является функцией координат системы
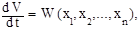 (2.6)
(2.6)
причем согласно свойству (2.2) эта функция W, так же как и сама V, тождественно обращается в нуль при x1 = x2 = ... = xn = 0. Поэтому к ней в одинаковой степени можно применять те же понятия знакоопределенности, знакопостоянства и знакопеременности в некоторой области вокруг начала координат.
Теорема Ляпунова об устойчивости нелинейных систем [2]: если при заданных в форме (2.1) уравнениях системы n-го порядка можно подобрать такую знакоопределенную функцию Ляпунова V(x1, x2, ..., xn ), чтобы ее производная по времени W(x1, x2, ..., xn ), тоже была знакоопределенной (или знакопостоянной), но имела знак, противоположный знаку V, то данная система устойчива; при знакоопределенной функции W будет иметь место асимптотическая устойчивость.
Теорема Ляпунова о неустойчивости нелинейных систем [2]: если при заданных в форме (2.1) уравнениях системы n-го порядка производная по времени W(x1, x2, ..., xn) от какой-нибудь функции Ляпунова V(x1, x2, ..., xn) окажется знакоопределенной, причем сама функция V в какой-нибудь области, примыкающей к началу координат, будет иметь знак, одинаковый со знаком производной W, то данная система неустойчива.
Замечания к теореме Ляпунова об устойчивости.
1. При заданных в форме (2.1) уравнениях системы выбор функции V неоднозначен, поэтому данная теорема Ляпунова обеспечивает получение достаточных условий устойчивости, которые не всегда будут и необходимыми, т.е. при выполнении условий теоремы система наверняка будет устойчивой, но эти условия могут не охватывать всей области устойчивости системы по параметрам.
2. Понятие устойчивости по Ляпунову допускает, что при знакоопределенной функции V производная от нее по времени W была не обязательно знакоопределенной или знакопостоянной, а могла быть и тождественно равна нулю. В результате система хотя и не будет асимптотически приближаться к установившемуся состоянию, но все же будет все время в достаточной близости от него.
Нелинейная система (рис. 2.1) с одним нелинейным элементом с однозначной статической характеристикой
yн = F(s)
в свободном состоянии может быть представлена в виде замкнутого контура, включающего в себя линейную часть (ЛЧ) и нелинейный элемент (НЭ) (рис. 2.5).
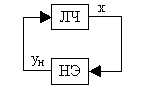
Рис. 2.5. Функциональная схема нелинейной системы
в свободном состоянии
При этом уравнения свободного движения системы (g = 0) будут
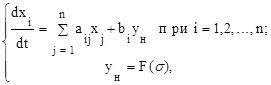 (2.7)
(2.7)
где 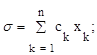
aij, bi, ck - постоянные коэффициенты.
Тогда задача исследования нелинейной системы (2.7) по Ляпунову сводится к определению функции V и ее производной
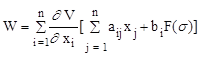 . (2.8)
. (2.8)
А.И.Лурье предложил функцию Ляпунова выбирать в виде суммы функции квадратичной формы L(x) и интеграла от нелинейной функции F(s) рассматриваемой системы
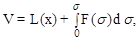 (2.9)
(2.9)
где 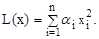
Нелинейная система называется абсолютно устойчивой, если она устойчива при любых начальных отклонениях и любой форме нелинейной характеристики, удовлетворяющей условиям:
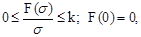 (2.10)
(2.10)
где k - заданное число.
Пример. Исследовать устойчивость системы, заданной уравнениями:
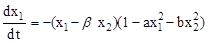 ;
;
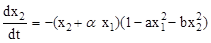 ,
,
где a, b, а, b - положительные постоянные числа.
Р е ш е н и е. Выбираем положительно-определенную функцию Ляпунова
V = ax12 + bx22 .
Находим производную от функции Ляпунова по времени
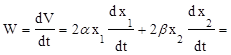
= -2ax1 (x1 - bx2 )(1 - ax12 - bx22) -2bx2 (x2 + ax1 )(1 - ax12 - bx22) =
= -2(1 - ax12 - bx22)( ax12 + bx22) .
Тогда W < 0 при (1 - ax12 - bx22 ) > 0 или ax12 + bx22 < 1.
Это достаточное условие устойчивости исследуемой нелинейной системы.
Границей устойчивости системы на плоскости ее координат (рис. 2.6) является эллипс
ax12 + bx22 = 1.

Рис. 2.6. Область устойчивости нелинейной системы
Дата добавления: 2015-06-01; просмотров: 2147;
