Положительная и отрицательная обратная связь. Коэффициенты реактивности.

Свойства устойчивости и саморегулируемости любой системы зависят от наличия обратных связей, их величины и знака. Любая система обладает свойством устойчивости только если ее обратные связи отрицательны (и плюс к тому хорошей управляемостью, если они достаточно малы по величине) .

Простейшей грубой моделью, иллюстрирующей эффект обратных связей, является перемещение по вертикали шарика на гладкой поверхности, получившего маленький импульс. Обратной связью здесь является сила тяжести. На плоской поверхности или в невесомости (нулевая обратная связь) он перемещается только по горизонтали. На поверхности типа параболы «ветвями вверх» после выведения из равновесия он будет совершать колебания относительно точки минимума (отрицательная обратная связь). На поверхности типа параболы «ветвями вниз» после выведения из равновесия он потеряет равновесие и скатится вниз (положительная обратная связь).

Обратные связи в реакторе называют эффектами реактивности, а характеризующие их коэффициенты - коэффициентами реактивности. Формальное математическое определение коэффициента реактивности α по произвольному параметру «P» (α_P)– это частная производная от реактивности α по «P» в окрестности параметра р₀

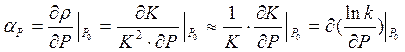
Эффектами реактивности называют разность реактивностей в двух разных (по любому параметру «P») состояниях реактора. Разные эффекты реактивности основаны обычно на эффектах в разных областях энергий и математически выражаются через разные коэффициенты формулы четырех сомножителей.

Из характеристик систем с обратными связями следует, что в реакторе обратные связи должны быть отрицательны (т.е при росте любого параметра «P» реактивность должна уменьшаться).

Выгода же от последней части этого выражения значительна, поскольку она позволяет на основе формулы четырех сомножителей для тепловых реакторов оценить вклад в коэффициент реактивности от каждой области энергии и каждого из сомножителей ибо, если К=( m j qn_а), то

a_р =¶(lnk¤¶р)= ¶(lnm ¤¶р) + ¶(lnj¤¶р) + ¶(lnq¤¶р)+ ¶(lnn_а ¤¶р) (5б)

Или

a_р =¶m¤(m¶р)+ ¶j¤(j¶р)+ ¶q¤(q¶р)+ ¶n_а ¤(n_а¶р). (5в)

Значит мы можем оценить и предсказать величину и знак вклада каждого из сомножителей по отдельности, причем в относительных величинах. Мы можем также заранее оценить зависимости каждого из слагаемых (5б-в) от параметра тесноты решетки и т.п. Приведем сначала общие выражения для каждого из коэффициентов (5), необходимых нам для анализа эффектов реактивности.

· Выражение для m достаточно громоздко, а главное, оно не используется при анализе и объяснении эффектов в тепловых реакторах.

· Выражение для вероятности избежать резонансного захвата при замедлении j

j= ЕХР(-N_топ I^u_а,эфф/N_зам(x s_s) _зам) , (6а)

где I^u_а,эфф -эффективный резонансный интеграл поглощения урана;