Пример выполнения курсового задания К 2
Дано: схема плоского механизма (рис. 2.25); уравнение движения груза 1: Х = 2·t2 + 2, см; радиусы колес: R2 = 50 см; r2 = 30 см; R3 = 60 см; r3 = 40 см. Определить кинематические характеристики точки М тела 3 в момент времени t1 = 1 c (VM(t1) = ?; 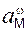 (t1) = ?;
(t1) = ?; 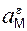 (t1) = ?
(t1) = ? 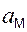 (t1) = ?).
(t1) = ?).

Решение. В начальный момент времени при t0 = 0 координата X(t0) = 2·(t0)2 + 2 = 2·02 + 2 = 2 см. Дифференцированием по времени уравнения движения груза 1 найдем проекцию 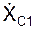 скорости его центра масс на ось ОХ:
скорости его центра масс на ось ОХ:
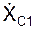 =
= 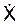 = dX/dt = d(2t2 + 2)/dt = 4·t.
= dX/dt = d(2t2 + 2)/dt = 4·t.
Так как 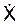 = 4·t > 0, то
= 4·t > 0, то 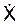 = V и, следовательно, координата Х = f(t) с течением времени увеличивается. Для графического построения определяемых кинематических характеристик изобразим механизм в произвольный момент времени t (рис. 2.26).
= V и, следовательно, координата Х = f(t) с течением времени увеличивается. Для графического построения определяемых кинематических характеристик изобразим механизм в произвольный момент времени t (рис. 2.26).
Так как груз 1 и участок АВ нити совершают поступательные движения, то справедливо равенство VB = V.
Точка В принадлежит телу 2, совершающему вращательное движение в системе отсчёта C2X2Y2Z2, поэтому модуль скорости этой точки определится из формулы VB = ω2·BC2 = ω2·r2 = I  I·r2, где ω2 – модуль угловой скорости
I·r2, где ω2 – модуль угловой скорости  тела 2. Согласно рис. 2.26 вращение тела 2 происходит против хода часовой стрелки. Определим модуль ω2 угловой скорости
тела 2. Согласно рис. 2.26 вращение тела 2 происходит против хода часовой стрелки. Определим модуль ω2 угловой скорости  тела 2 по формуле ω2 = VB/r2 = V/r2. По известному модулю ω2 угловой скорости тела 2 определяется модуль VC скорости точки С тела 2:
тела 2 по формуле ω2 = VB/r2 = V/r2. По известному модулю ω2 угловой скорости тела 2 определяется модуль VC скорости точки С тела 2:

VC = ω2·CC2 = ω2·R2 = (V/r2)·R2 = V·(R2/r2).
Так как участок нити CD совершает поступательное движение, то справедливо равенство VC = VD = V·(R2/r2). С другой стороны, точка D принадлежит колесу 3. Исходя из условия принадлежности этой точки телу 3, имеем VD = ω3·R3 = V·(R2/r2), где ω3 – модуль угловой скорости 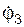 тела 3. Тело 3 осуществляет вращение в направлении хода часовой стрелки. Его угловая скорость вычисляется по формуле
тела 3. Тело 3 осуществляет вращение в направлении хода часовой стрелки. Его угловая скорость вычисляется по формуле
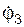 =
= 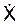 ·(R2/(r2·R3)) = (4·t)·(R2/(r2·R3)).
·(R2/(r2·R3)) = (4·t)·(R2/(r2·R3)).
По известной угловой скорости 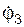 тела 3, находят его угловое ускорение
тела 3, находят его угловое ускорение 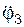 .
.
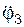 = d
= d 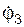 /dt = 4·(R2/(r2·R3)) = const > 0.
/dt = 4·(R2/(r2·R3)) = const > 0.
Так как 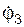 > 0 и
> 0 и 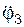 = const > 0, то происходит равноускоренное вращение тела 3. Определяем кинематические характеристики точки М тела 3 в момент времени (t1).
= const > 0, то происходит равноускоренное вращение тела 3. Определяем кинематические характеристики точки М тела 3 в момент времени (t1).
Модуль угловой скорости
ω3(t1) = I 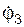 (t1)I = (4·t1)·(R2/(r2·R3)).
(t1)I = (4·t1)·(R2/(r2·R3)).
Модуль углового ускорения
ε3(t1) = 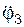 = 4·(R2/(r2·R3)).
= 4·(R2/(r2·R3)).
Модуль скорости точки М равна
VM(t1) = ω3(t1)·MC3 = ω3(t1)·r3 = (4·t1)·(R2·r3/(r2·R3)).
Модуль центростремительного ускорения точки М
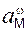 (t1) = (ω3(t1))2·MC3 = (ω3(t1))2·r3 = (4·t1·(R2/(r2·R3)))2·r3.
(t1) = (ω3(t1))2·MC3 = (ω3(t1))2·r3 = (4·t1·(R2/(r2·R3)))2·r3.
Модуль вращательного ускорения равен
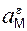 (t1) = ε3(t1)·r3 = 4·(R2·r3/(r2·R3)).
(t1) = ε3(t1)·r3 = 4·(R2·r3/(r2·R3)).
Модуль полного ускорения точки М
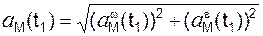 .
.
Произведём вычисления для момента времени t1 = 1 c и полученные значения сведём в таблицу.
Таблица
| ω3(t1), рад/с | ε3(t1), рад/с2 | VM(t1), см/с | 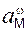 (t1), см/с2 (t1), см/с2
| 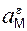 (t1), см/с2 (t1), см/с2
| 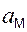 (t1), см/с2 (t1), см/с2
|
| 1,111 | 1,111 | 44,444 | 49,382 | 44,444 | 66,434 |
Кинематические характеристики точки М показаны на рис. 2.26.
2.18. Плоскопараллельное движение твёрдого тела
Плоскопараллельным (плоским) движением твёрдого тела называется такое движение, при котором каждая точка тела движется в плоскости, параллельной некоторой неподвижной плоскости.
Плоскопараллельные движения совершают многие тела механизмов и машин, например, катящееся колесо, шатун в кривошипно-ползунном механизме и др.
Рассмотрим сечение S1 тела плоскостью O1X1Y1 подвижной системы отсчёта O1X1Y1Z1, плоскости которой параллельны плоскостям неподвижной системы отсчёта OXYZ (рис. 2.27).
При плоскопараллельном движении все точки тела, лежащие на прямой А1А2, перпендикулярной сечению S1, движутся одинаково и, следовательно, траектории этих точек совпадают при наложении друг на друга, а скорости и ускорения их геометрически равны, т. е.
VA = VA1 = VA2;
aA= aA1= aA2 .


Это позволяет свести изучение плоскопараллельного движения тела к изучению движения плоской фигуры в неподвижной системе отсчёта OXY (рис. 2.28).
Так как положение плоской фигуры в системе отсчёта OXY полностью определяется положением отрезка АВ, то движение плоской фигуры можно изучать как движение прямолинейного отрезка АВ. Как видно из рис. 2.28, при плоскопараллельном движении тела траектории движения точек различны и, следовательно, скорости и ускорения точек геометрически различны.
Таким образом, плоскопараллельное движение тела заменяется рассмотрением движения прямолинейного отрезка АВ в системе отсчёта OXY.

Плоскопараллельное движение тела можно представить как вращательное движение относительно подвижной оси, проходящей через полюс. На рис. 2.29 за полюс принята точка А, в которую помещено начало подвижной системы отсчёта AX1Y1, совершающей поступательное движение.
Через точку А проходит подвижная ось вращения AZ1, перпендикулярная плоскости OXY (рис. 2.29). Положение отрезка АВ в неподвижной системе отсчёта полностью определяется тремя уравнениями:
XA = f1(t); YA = f2(t); φ = f3(t).
Эти уравнения и называют уравнениями плоскопараллельного движения твёрдого тела. При этом два уравнения: XA = f1(t); YA = f2(t) описывают поступательную часть движения тела со скоростью VA и ускорением aA полюса А, а третье уравнение описывает вращательную часть движения с угловой скоростью 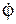 и угловым ускорением
и угловым ускорением 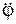 относительно подвижной оси вращения AZ1, проходящей через полюс А.
относительно подвижной оси вращения AZ1, проходящей через полюс А.
Таким образом, плоскопараллельное движение тела представляет собой сумму двух движений: поступательное движение тела со скоростью полюса А и вращательное движение с угловой скоростью 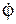 относительно оси, проходящей через полюс А. За полюс можно принять любую точку тела. Как правило, за полюс принимается центр масс тела.
относительно оси, проходящей через полюс А. За полюс можно принять любую точку тела. Как правило, за полюс принимается центр масс тела.
Зная уравнения плоскопараллельного движения тела: XA = f1(t); YA = f2(t); φ = f3(t), несложно определить скорость VA и ускорение aA полюса А, а также угловую скорость 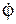 и угловое ускорение
и угловое ускорение 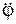 по формулам:
по формулам:
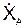 = dXA/dt;
= dXA/dt; 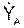 = dYA/dt;
= dYA/dt; 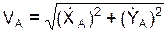 ;
;
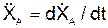 = d2XA/dt2;
= d2XA/dt2; 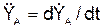 = d2YA/dt2;
= d2YA/dt2;
aA = 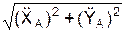 ;
; 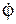 = dφ/dt;
= dφ/dt; 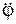 = d2φ/dt2.
= d2φ/dt2.
При вращении тела относительно оси, проходящей через полюс А (см. рис. 2.29), точка В описывает окружность радиусом, равным длине отрезка АВ. Зависимость между скоростями точек плоской фигуры устанавливается по следующей теореме.
Теорема. Скорость любой точки В плоской фигуры в неподвижной системе отсчёта OXY равна геометрической сумме скорости полюса А и скорости этой точки в её вращательном движении вместе с плоской фигурой относительно оси, проходящей через полюс:
VB = VA + VBA.
Модуль VBA вращательной скорости VBA находится по формуле
VBA = ω·BA,
где ω – модуль угловой скорости 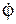 тела.
тела.
При этом VBA ┴ ВА. Модуль скорости точки В находят по формуле
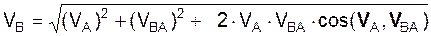 .
.
На рис. 2.30 представлен пример определения скорости VB произвольной точки В по исходным данным, приведенным на рис. 2.29.
Определение скоростей точек тела с помощью формулы
VB = VA + VBA
связано с довольно сложными расчётами. Однако, исходя из этого основного результата, можно получить ряд других, практически более удобных и простых методов определения скоростей точек тела. Одним из этих методов является теорема: проекции скоростей точек тела на прямую, соединяющую эти точки, равны друг другу.

Согласно этой теореме имеем VA·cos(α) = VВ·cos(β) (рис. 2.31).

Этот результат позволяет легко находить скорость данной точки тела, если известны направление движения этой точки и скорость какой-нибудь другой точки того же тела.
Дата добавления: 2015-05-30; просмотров: 873;
