С помощью мгновенного центра скоростей

Другой простой и наглядный метод определения скоростей точек при плоскопараллельном движении тела основан на понятии мгновенного центра скоростей.

Мгновенным центром скоростей (МЦС) называется точка сечения S тела, скорость которой в данный момент времени равна нулю.

Легко убедиться в том, что если тело движется не поступательно, то такая точка в каждый момент времени существует и притом единственная.

Пусть заданы скорости V_A и V_B двух точек А и В тела. Тогда точка Р, лежащая на пересечении перпендикуляров к соответствующим векторам V_A и V_B будет мгновенным центром скоростей, так как V_Р = 0 (рис. 2.32).

Таким образом, в каждый момент времени плоскопараллельное движение тела можно представить как вращательное относительно оси, проходящей через МЦС. Исходя из этого, имеем:

V_A = ω·AP; V_{A ┴} AP; V_B = ω·BP; V_{B ┴} BP,

где ω – модуль угловой скорости 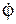тела.

Отсюда следует V_A/AP = V_B/BP = ω, т. е. модули скоростей точек тела пропорциональны их расстояниям до мгновенного центра скоростей.

Полученные результаты приводят к следующим выводам:

1) для определения мгновенного центра скоростей надо знать только направления скоростей V_A и V_B каких-нибудь двух точек А и В тела (или траектории этих точек). МЦС находится в точке пересечения перпендикуляров, восстановленных в точках А и В к скоростям этих точек (или к касательным к траекториям);

2) для определения скорости любой точки тела надо знать модуль и направление скорости какой-нибудь точки А тела и направление скорости другой его точки В. Тогда, восстановив из точек А и В перпендикуляры к V_A и V_B, определим МЦС (точку Р) и по направлению V_A найдем направление поворота тела. После того, зная V_A, найдем скорость V_В любой точки тела. Направлен вектор V_В перпендикулярно ВР (V_{В ┴} ВР) в сторону поворота тела;

3) модуль угловой скорости тела равен отношению модуля скорости какой-нибудь точки к её расстоянию до мгновенного центра скоростей: ω = V_A/АР = V_В/ВР = V_С/СР = ….