Аксиомы статики
СТАТИКА
Основные понятия статики
В основу каждого раздела механики положен ряд понятий и определений, принята система аксиом, т. е. важнейших положений, многократно подтверждённых практикой. Приступая к изучению статики, следует определить основные понятия, встречающиеся в этом разделе механики.
Статика – раздел механики, в котором изучают условия равновесия механических систем под действием сил.
Масса – одна из основных характеристик любого материального объекта, определяющая его инертные и гравитационные свойства.
Масса является мерой инертности точки и мерой инертности тела при его поступательном движении. Масса измеряется в кг.
Инертность – свойство материального тела, проявляющееся в сохранении движения, совершаемого им при отсутствии действующих сил, и в постепенном изменении этого движения с течением времени, когда на тело начинают действовать силы.
Материальная точка – точка, имеющая массу.
Материальная точка не имеет размеров и обладает способностью взаимодействовать с другими материальными точками.
Абсолютно твёрдое тело – материальное тело, в котором расстояние между двумя любыми точками остается неизменным (рис. 1.1).
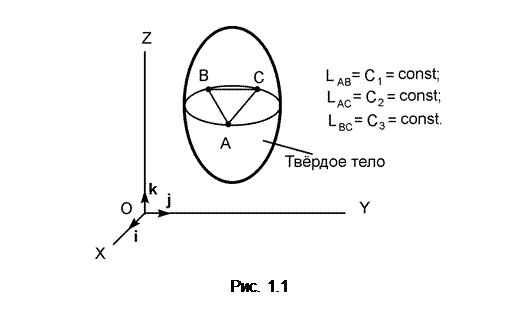 |
В природе такие тела отсутствуют, так как каждое тело деформируется в результате приложенных воздействий. Однако принятое допущение (абсолютно твёрдое тело) значительно упрощает изучение действия сил на тело и условий, при которых эти силы уравновешиваются. В дальнейшем абсолютно твёрдые тела условлено называть телами.
Механическая система – любая совокупность материальных точек.
Движения материальных точек в механической системе взаимозависимы. В механике тело рассматривают как механическую систему, образованную непрерывной совокупностью материальных точек. Тела могут взаимодействовать друг с другом.
Механическое действие – действие на данное тело со стороны других тел, которое приводит к изменению скоростей точек этого тела или следствием которого является изменение взаимного положения точек данного тела.
Другими словами, при механическом действии тело приобретает механическое движение.
Механическое движение – изменение с течением времени взаимного положения тел в пространстве или взаимного положения частей данного тела.
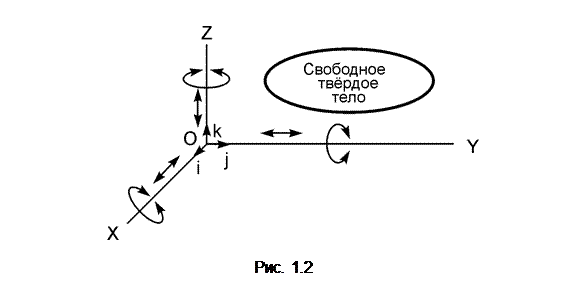 |
Таким образом, тело либо деформируется, либо перемещается в пространстве. Деформацию тел изучает наука – сопротивление материалов. Так как в теоретической механике имеют дело с абсолютно твёрдыми телами, то при механическом действии тела изменяют свое положение в пространстве относительно друг друга. В общем случае тело может поступательно перемещаться в пространстве по трём направлениям (параллельно координатным осям OX, OY, OZ) и вращаться относительно этих осей (рис. 1.2).
Свободное тело – тело, на перемещения которого в пространстве не наложено никаких ограничений.
Следовательно, свободное тело может осуществлять в системе отсчёта OXYZ шесть движений. Другими словами, тело имеет шесть степеней свободы.
Тело может находиться в состоянии покоя, которое является частным случаем механического движения, когда скорости точек рассматриваемого тела равны нулю. Если тело покоится, то говорят, что оно находится в состоянии равновесия.
Равновесие механической системы – состояние механической системы, при котором её точки под действием приложенных сил остаются в покое по отношению к рассматриваемой системе отсчёта.
Система отсчёта – система координат, связанная с телом, по отношению к которому определяется положение других тел (механических систем) в разные моменты времени.
Важнейшим понятием в теоретической механике является понятие силы.
Сила – векторная величина, являющаяся мерой механического действия одного тела на другое.
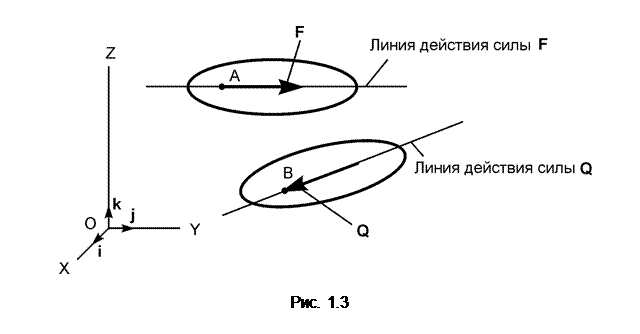
Сила как вектор определяется тремя элементами: числовым значением (модулем), направлением и точкой приложения. Графически силу изображают направленным прямолинейным отрезком (вектором), совпадающим по направлению с направлением силы (рис. 1.3).
|
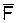 ,
,  ,
,  .
.
Линия действия силы – прямая линия, вдоль которой направлен вектор, изображающий силу.
Простейшим примером силы является сила тяжести, с которой тело притягивается к Земле.
Сила тяжести – сила, действующая на материальную точку вблизи земной поверхности, равная произведению массы m этой точки на ускорение gсвободного падения в вакууме.
G= m·g.
Сила тяжести G прикладывается в центре С тяжести тела и направлена к центру Земли (по вертикали). В неподвижной (НСО) относительно Земли системе отсчёта OXYZ сила тяжести тела изображается так, как это показано на рис. 1.4.
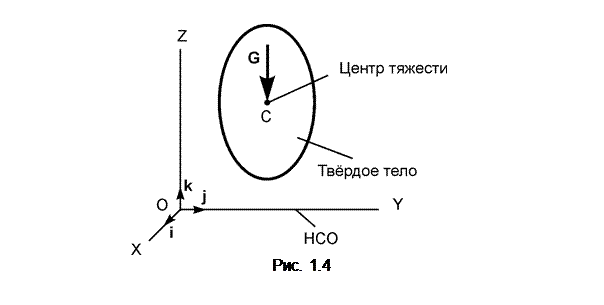
Если речь идет о величине (модуле) силы тяжести тела, то употребляют термин «вес тела».
Вес тела – сумма модулей сил тяжести, действующих на частицы этого тела.
Вес G тела находят по формуле
G = m·g.
Силы имеют различную физическую природу, например, сила давления пара, сила притяжения наэлектризованных тел и т. д. В теоретической механике не рассматривают физическую природу сил, здесь важны только величина, направление и точка приложения силы. Модуль силы измеряют в ньютонах [H].
Силы, действующие на механическую систему, делят на две группы: внешние и внутренние.
Внешняя сила – сила, действующая на какую-либо точку механической системы со стороны тел, не принадлежащих рассматриваемой механической системе.
Внешние силы принято обозначать символами: FiE, RiE.
Внутренние силы – силы, действующие на какие-либо точки механической системы со стороны других точек, принадлежащих рассматриваемой механической системе.
Внутренние силы принято обозначать символом RiJ.
Система сил – любая совокупность сил, действующих на механическую систему.
Систему сил принято обозначать (F1,…,Fn).
Уравновешенная система сил – система сил, которая будучи приложена к свободному телу, находящемуся в равновесии, не выводит его из этого кинематического состояния.
Уравновешивающая система сил – система сил, которая вместе с заданной другой системой сил составляет уравновешенную систему сил.
Эквивалентные системы сил – две или несколько систем сил, имеющих одну и ту же уравновешивающую систему сил.
Эквивалентные системы сил приводят свободное тело в одно и то же кинематическое состояние. Для обозначения эквивалентности систем сил используют знак «~».
Равнодействующая системы сил – сила, эквивалентная данной системе сил.
Плоская система сил – система сил, линии действия которых расположены в одной плоскости.
Сходящаяся система сил – система сил, линии действия которых пересекаются в одной точке.
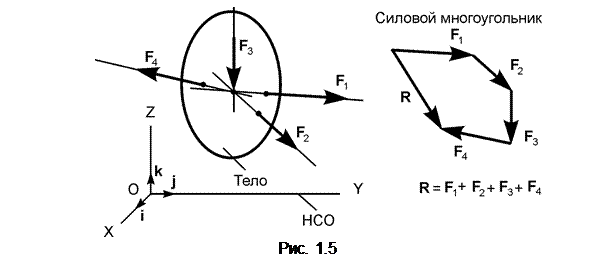
Из курса физики известно, что равнодействующая сходящейся системы сил графически определяется по правилу силового многоугольника (рис. 1.5).
При построении силового многоугольника равнодействующая R соединяет начало первого вектора с концом последнего. Силовой многоугольник не замкнут.
Таким образом, сходящаяся система сил имеет равнодействующую R, определяемую векторным равенством:
R =F1 +…+ F4.
В общем случае для системы сходящихся сил (F1,…,Fn) используют векторное равенство R = Σ Fi.
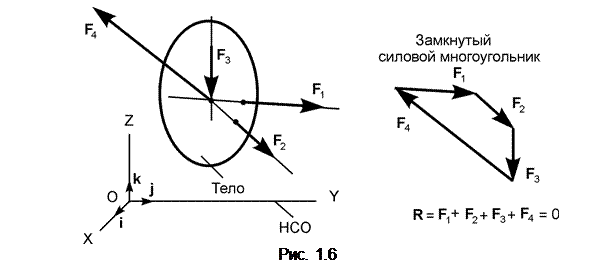
Уравновешенную систему сил графически изображают замкнутым силовым многоугольником, в котором конец последнего вектора приходит в начало первого вектора (рис. 1.6).
Такую систему сил описывают равенством R = F1 +…+ F4 = 0. В общем случае для уравновешенной системы сил (F1,…,Fn) справедливо равенство R = Σ Fi = 0.
Силы делят на сосредоточенные и распределённые.
Сосредоточенная сила – сила, приложенная к телу в какой-либо одной его точке.
Распределённые силы – силы, действующие на все точки некоторой части линии, поверхности или объёма.
Понятие о сосредоточенной силе является условным, так как практически приложить силу в точке нельзя. Силу, которую в механике рассматривают как сосредоточенную, представляет собой равнодействующую некоторой системы распределённых сил.
Распределённые силы характеризуются величиной q интенсивности распределения силы, т. е. величиной силы на единицу объёма, поверхности или длины линии. Интенсивность распределения силы может иметь следующие размерности: Н/м3; Н/м2; Н/м. На тела в основном действуют параллельные и сходящиеся распределённые силы. К параллельным силам, распределённым по объёму, относятся силы тяжести частиц тела.
Поскольку все аксиомы и теоремы статики формулируются для сосредоточенных сил, необходимо рассмотреть способы перехода от распределённых сил к сосредоточенным силам.
Рассмотрим замену линейно распределённых сил сосредоточенной силой.
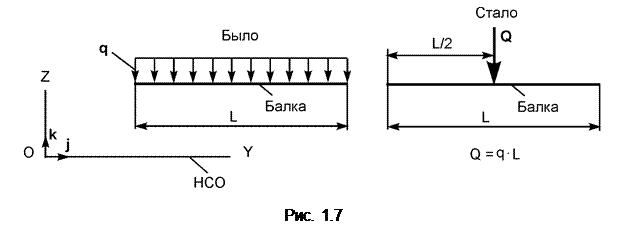
Равнодействующую распределённых на линии параллельных сил постоянной интенсивности q определяют по формуле Q = q×L, где L – длина балки (рис. 1.7).
Равнодействующая распределённых сил (сосредоточенная сила) прикладывается к балке под центром тяжести площади прямоугольника.
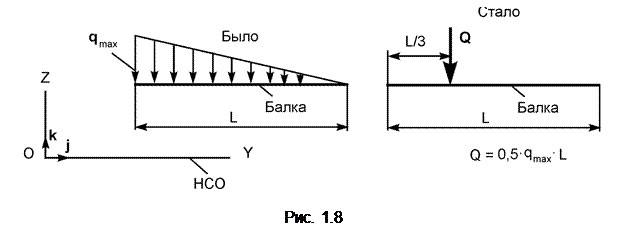
В инженерной практике часто применяют нагрузку, интенсивность которой изменяется по закону треугольника (рис. 1.8).
Равнодействующую параллельных распределённых сил на линии с интенсивностью, изменяющейся по закону треугольника, определяют по формуле Q = 0,5qmax×L, где qmax – наибольшая интенсивность. Линия действия сосредоточенной силы Q смещена в сторону наибольшей интенсивности и проходит через центр тяжести площади треугольника.
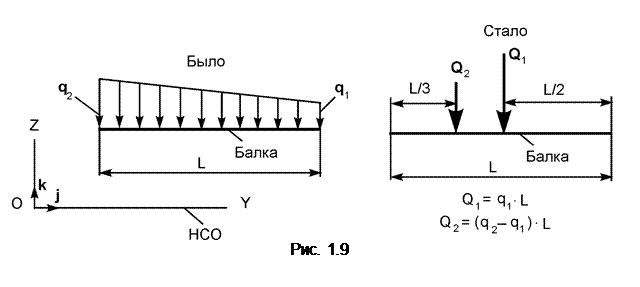
В более сложных случаях распределённые нагрузки заменяют несколькими сосредоточенными силами. Пример такой замены приведен на рис. 1.9.
Модули Q1, Q2 сил Q1, Q2 определяют по формулам:
Q1 = q1·L; Q2 = 0,5·(q2 – q1)·L.
Аксиомы статики
1. Аксиома инерции. Под действием уравновешенной системы сил (ΣFi = 0 или (F1,…, Fn) ~ 0) свободное тело находится в состоянии покоя или равномерного прямолинейного движения.
2. 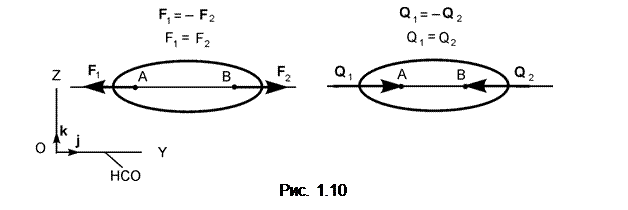
Аксиома равновесия двух сил. Две силы, приложенные к телу, уравновешиваются только в том случае, если их модули равны и они направлены по одной прямой в противоположные стороны (рис. 1.10).
3. Аксиома присоединения и исключения уравновешенной системы сил. Действие системы сил на тело не изменится, если к ней присоединить или из неё исключить уравновешенную систему сил.
Дата добавления: 2015-05-30; просмотров: 2651;
