Аксиомы статики.
Данные аксиомы сформулированы на основе наблюдения и изучения окружающих нас явлений реального мира. Некоторые основные законы механики Галилея – Ньютона являются одновременно и аксиомами статики.
1. Аксиома инерции.
Под действием взаимно уравновешивающихся сил материальная точка (тело) находится в состоянии покоя или движется прямолинейно и равномерно. Равномерное и прямолинейное движение материальной точки является движением по инерции.
2. Аксиома равновесия двух сил
Две силы, приложенных к телу, взаимно уравновешиваются только в том случае, если их модули равны и если они направлены по одной прямой в противоположные стороны.
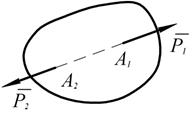
Рис. 1.4
3. Аксиома присоединения и исключения уравновешивающихся сил.
Действие системы сил на твёрдое тело не изменяется, если к ней присоединить или из неё исключить систему взаимно уравновешивающихся сил.
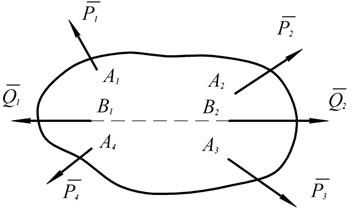
Рис. 1.5
Пусть к твёрдому телу приложены силы 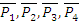 , под действием которых тело находится в покое или совершает какое-то движение. Приложим к телу равные противоположно направленные силы
, под действием которых тело находится в покое или совершает какое-то движение. Приложим к телу равные противоположно направленные силы 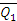 и
и 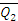 , которые взаимно уравновешиваются.
, которые взаимно уравновешиваются.  Если тело находится в движении, то оно будет двигаться под действием новой системы сил
Если тело находится в движении, то оно будет двигаться под действием новой системы сил 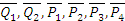 так же и под действием сил
так же и под действием сил 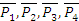 , то есть основная система сил эквивалентна прежней.
, то есть основная система сил эквивалентна прежней.
Следствие. Не нарушая состояния абсолютно твёрдого тела, силу можно переносить вдоль линии её действия, сохраняя неизменными её модуль и направление.
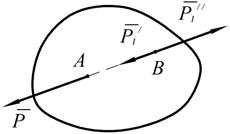
Рис. 1.6
Предположим в т. А приложена 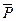 . Приложим в точке В две силы
. Приложим в точке В две силы 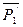 и
и 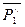 равные по модулю силе
равные по модулю силе 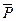 и направленные по линии действия
и направленные по линии действия 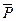 в противоположные стороны. Затем отбросим силы
в противоположные стороны. Затем отбросим силы 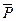 и
и 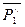 как взаимно- уравновешивающееся. Тогда к телу в точке В будет приложена сила
как взаимно- уравновешивающееся. Тогда к телу в точке В будет приложена сила 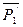 =
= 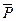 .
.
Таким образом, силу можно переносить в любую точку по линии действия, не изменяя её модуля и направления. Поэтому в статике сила рассматривается как скользящий вектор.
4. Аксиома параллелограмма сил
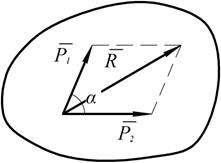 Равнодействующая двух пересекающихся сил приложена в точке их пересечения и изображается диагональю параллелограмма, построенного на этих силах.
Равнодействующая двух пересекающихся сил приложена в точке их пересечения и изображается диагональю параллелограмма, построенного на этих силах.
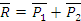
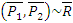
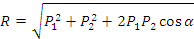
Рис. 1.7
5. Аксиома равенства действия и противодействия
Всякому действию соответствует равное и противоположно направленное противодействие. Эта аксиома утверждает, что силы действия друг на друга двух сил равны по модулю и направлены в противоположные стороны. Аксиома установлена Ньютоном.
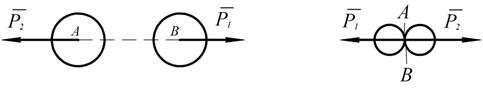
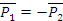
Рис. 1.8 Рис. 1.9
В природе не существует одностороннего действия сил. Силы, действующие и противодействующие, приложены к разным телам, потому они не уравновешиваются.
6. Аксиома сохранения равновесия сил, приложенных к деформирующемуся телу при его затвердевании
Равновесие сил, приложенных к деформирующемуся телу, сохраняется при его затвердении. Из этой, аксиомы следует, что условие равновесия сил приложенных к абсолютно твёрдому телу, должны и сохраняться для сил, приложенных к деформирующемуся телу. Однако в случае деформированного тела эти условия необходимы, но не достаточны.
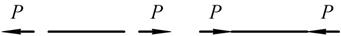
Рис. 1.10
1.3. Несвободное твёрдое тело
Твёрдое тело, на перемещение которого не наложено никаких ограничений, называется свободным. Тело, ограничивающее свободу движения данного твёрдого тела, является по отношению к нему связью.
Твёрдое тело, свобода движения которого ограничена связями, называется несвободным. Всякое связанное тело можно представить свободным, если связи заменить их реакциями (принцип освобождаемости твёрдых тел от связей).
Все связи можно разделить на несколько типов.
1. Идеально гладкая поверхность.
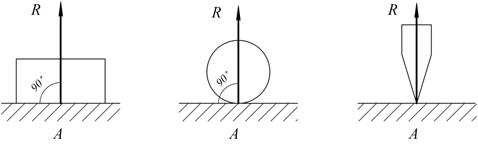
Рис. 1.11
Реакции опоры, приложены в точке опоры, всегда направлены перпендикулярно опоре.
2. Гибкая связь (трос, нить, цепь, канат)
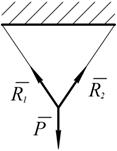
Рис. 1.12
Реакция гибкой нити, направлена на нити к точке подвеса.
3. Жёсткий стержень
На схемах показывается толстой линией. Реакция стержня направлена вдоль стержня. Стержень может быть сжат или растянут. Точное направление реакции определяют, мысленно убрав стержень и анализируя направление перемещение узла.
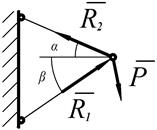 |
Рис. 1.13
4. Брус.
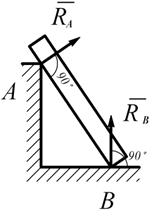
Рис. 1.14
5. Цилиндрическая шарнирно – неподвижная опора
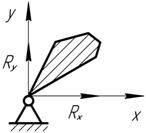
Рис. 1.15
6. Цилиндрическая шарнирно – подвижная опора
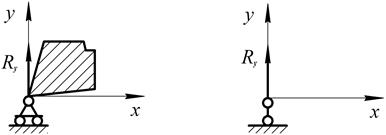
Рис. 1.16
7. Защемление (заделка)
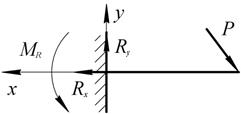
Рис. 1.17
8. Невесомый стержень, на концах которого шарниры
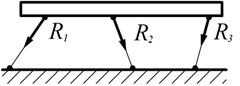
Рис. 1.18
9. Сферический шарнир
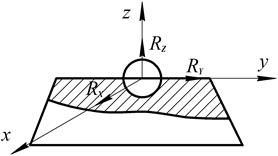
Рис. 1.19
10. Подпятник
(Совокупность цилиндрического шарнира и упорной поверхности)
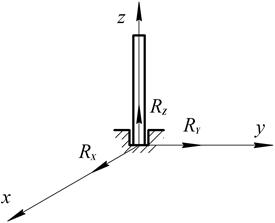
Рис. 1.20
Дата добавления: 2015-06-17; просмотров: 2219;
