Проекции силы на ось и плоскость
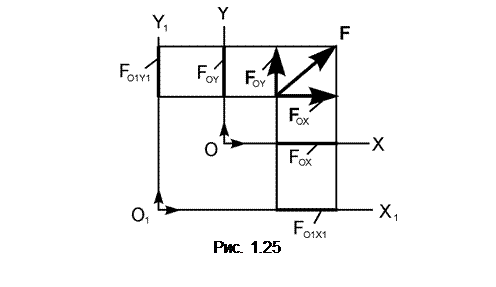 |
Пусть линия действия силы F лежит в плоскости OXY (рис. 1.25).
По правилу параллелограмма разложим эту силу на составляющие силы FОХ, FOY по координатным осям OX и OY. Силы FOX, FOY называют компонентами силы Fпо координатным осям OX и OY. Очевидно векторное равенство
F = FOX + FOY.
Спроецируем компоненты FOX, FOY силы F на координатные оси и получим скалярные величины FOX, FOY, которые называют проекциями силы на оси OX и OY.
Компоненты силы и её проекции на координатные оси связаны равенствами: FOX = i×FOX; FOY = j×FOY.
Проекция силы на ось – скалярная величина, равная взятой со знаком плюс или минус длине отрезка, заключённого между проекциями на ось начала и конца силы.
Из определения следует, что проекции данной силы на любые параллельные оси равны друг другу: FOX = FO1X1, FOY = FO1Y1, где FO1X1, FO1Y1 – проекции силы F на координатные оси системы отсчёта O1X1Y1.
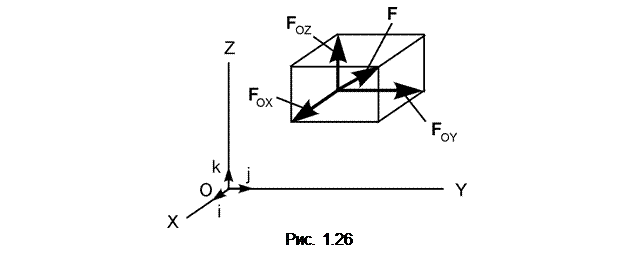
Пусть в пространстве в системе отсчёта OXYZ задана сила F, (рис. 1.26).
Используя правило параллелепипеда, разложим силу F на компоненты FOX, FOY, FOZ. По правилу сложения векторов справедливо равенство
F = FOX + FOY + FOZ.
Компоненты FOX, FOY, FOZ силы F связаны с их проекциями FOX, FOY, FOZ на координатные оси соотношениями: FOX = i×FOX; FOY = j×FOY; FOZ = k×FOZ. Следовательно, справедливо равенство
F = i·FOX + j·FOY + k·FOZ.
Последнее равенство представляет собой формулу разложения силы на составляющие силы по координатным осям.
Проекция силы на координатную ось равна произведению модуля силы на косинус угла, составленного направлениями силы и оси.
FOX = F×cos(F, i); FOY = F×cos(F, j); FOZ = F×cos(F, k).
Модуль силы через её проекции определяют по формуле
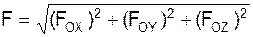 .
.
Направляющие косинусы, используемые для определения направления силы, находят по формулам:
cos(F, i) = FOX/F; cos(F, j) = FOY/F; cos(F, k) = FOZ/F.
Если рассматривается сила, лежащая в плоскости OXY, то применяются формулы:
F = FOX + FOY;
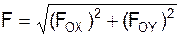 ;
;
cos(F, i) = FOX/F; cos(F, j) = FOY/F.
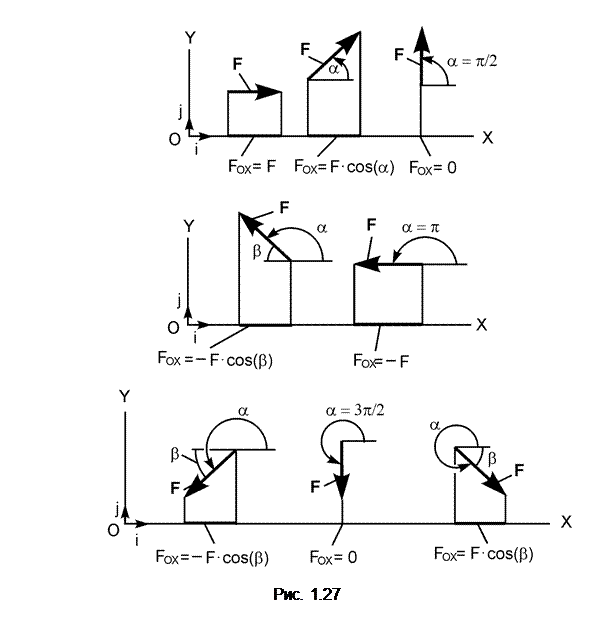
При определении проекции силы на ось возможны следующие частные случаи (рис. 1.27).
Анализ частных случаев определения проекции силы на ось позволяет сделать следующие выводы: 1) если сила и ось направлены в одну полуплоскость, то проекция силы на ось положительна; 2) если сила и ось направлены в разные полуплоскости, то проекция силы на ось отрицательна; 3) если сила и ось взаимно перпендикулярны, то проекция силы на ось равна нулю; 4) если сила и ось параллельны, то сила проецируется на ось в натуральную величину с соответствующим знаком.
При решении задач статики рекомендуется вычислять абсолютное значение проекции как произведение модуля силы на косинус острого угла между линией действия силы и осью, определяя знак проекции непосредственно по чертежу.
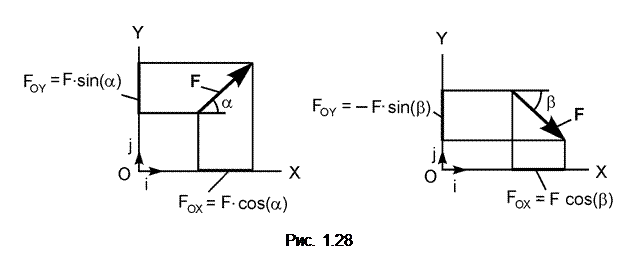
В инженерной практике принято использовать заданный угол и выражать через него проекции силы на оси (рис. 1.28).
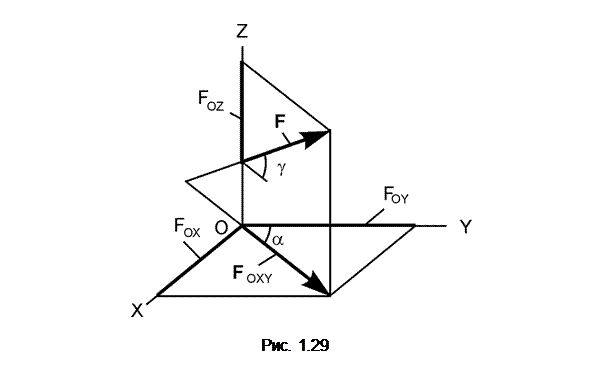
Проекцией силы на плоскость OXY называется вектор FOXY, заключенный между проекциями начала и конца силы F на эту плоскость (рис. 1.29).
Таким образом, в отличие от проекции силы на ось, проекция силы на плоскость есть величина векторная, так как она характеризуется не только модулем, но и направлением по плоскости OXY. По модулю FОXY = F·cos(g), где g – угол между направлением силы F и её проекцией FOXY,
 |
В некоторых случаях для нахождения проекции силы на ось бывает удобнее найти сначала её проекцию на плоскость, в которой эта ось лежит, а затем найденную проекцию силы на плоскость спроецировать на данную ось. Тогда:
FOX = FOXY·sin(α) = F·cos(g)·sin(α);
FOY = FOXY·cos(α) = F·cos(g)·cos(α);
FOZ = F·sin(g).
Дата добавления: 2015-05-30; просмотров: 3493;
