Симплексный метод
Симплексный метод или метод последовательного улучшения плана является одним из основных методов решения задач ЛП. название симплексный метод берет от слова «симплекс», которым создатель метода Р. Данциг обозначил наложенное на переменные x1, x2 ... xn ограничение x1+x2+ ... +xn=1.
þ В математике симплексом в k-мерном пространстве называется совокупность k+1 вершин.
Так для плоскости при k=2 симплексом будет треугольник; в пространстве при k=3 симплексом будет тетраэдр, имеющий 4 вершины.
С учетом этого понятия аналитический метод решения задачи ЛП называют симплекс-методом. Он основан на алгоритме направленного перебора вершин. Этот алгоритм обеспечивает переход от одной вершины к другой в таком направлении, при котором значение целевой функции от вершины к вершине улучшается.
þ Определение значения целевой функции и переменных в одной вершине считается итерацией.
Число итераций в реальных задачах может измеряться сотнями. Вручную, с помощью симплекс-метода, могут быть решены задачи, содержащие не более 10 итераций. Поэтому в реальных задачах применяют ЭВМ и пакеты прикладных программ (ППП).
Метод решения задач ЛП с помощью симплексных таблиц изложен на конкретном примере. Пусть требуется найти неотрицательное решение системы линейных неравенств:
ì4x1+9x2 £ 56
(5.14) í5x1+3x2 £ 37
î-x1+2x2 £ 2
обращающее в максимум линейную форму:
¦=3x1+4x2 (5.15)
Вначале перейдем от системы неравенств (5.14) к системе уравнений, добавив к левым частям неравенств неотрицательные переменные x3, x4, x5. Мы получим:
ì4x1+9x2+x3+0 . x4+0 . x5=56
(5.16) í5x1+3x2+0 . x3+x4+0 . x5=37
î-x1+2x2+0 . x3+0 . x4+ x5=2
¦= 3x1+4x2+0 . x3+0 . x4+0 . x5 (5.17)
перепишем теперь систему (5.16) в виде системы 0-уравнений:
ì0=56 - (4x1+9x2+1 . x3+0 . x4+0 . x5)
(5.18) í0=37 - (5x1+3x2+0 . x3+1 . x4+0 . x5)
î0=2 - (-x1+2x2+0 . x3+0 . x4+1 . x5)
¦=0 - (-3x1-4x2-0 . x3-0 . x4-0 . x5) (5.19)
заметим, что система (5.18) может быть записана в виде одного векторного равенства:
0=B-(A1x1+A2x2+A3x3+A4x4+A5x5),
где вектор-столбец В имеет своими компонентами свободные члены, а векторы A1, A2, ... , A5 - коэффициенты при соответствующих переменных x1, x2, x3, x4, x5. Иными словами:
| В= | A1= | A2= | A3= | A4= | A5= | |||||||||||
| -1 |
Линейная форма имеет вид: ¦=3x1+4x2+0 . x3+0 . x4+0 . x5.
Векторы A3, A4, A5 образуют базис. Это означает, что, присвоив х1=0, х2=0, получаем из (5.16) первое базисное решение: x1=0; x2=0; x3=56; x4=37; x5=2.
При этом значение линейной формы ¦=0. На основании (5.18) строим первую симплексную таблицу.
Симплексная таблица строится следующим образом:
В заглавной строке пишем последовательно векторы B, A1, A2, A3, A4 , A5. Слева добавляем колонку «Базисные векторы», рядом с ней колонку «С», в которой поставлены коэффициенты при базисных переменных в линейной форме, в данном случае величины С3, С4, С5. В последней строке, называемой индексной, и обозначаемой через ¦ j-Сj, проставляются числа, равные значению линейной формы, в соответствием с уравнением (j=1, 2, 3, 4, 5). В итоге мы имеем таблицу 5.3.
Таблица 5.3.
| Базисные | Коэффициенты | Вектор свободных | |||||
| векторы | линейной формы С | членов В | A1 | A2 | A3 | A4 | A5 |
| A3 | |||||||
| A4 | |||||||
| A5 | -1 | ||||||
| Индексная строка ¦ j-Сj | -3 | -4 |
Это первая симплексная таблица, соответствующая первому базисному решению: x1=0; x2=0; x3=56; x4=37; x5=2. Значение линейной формы, равное нулю, мы записываем в первой клетке индексной строки.
Т.к. мы решаем задачу на максимум, то из выражения линейной формы видно, что имеет смысл увеличить x1 или x2. Действительно, коэффициенты при этих переменных в скобках отрицательны (а по существу положительны), и если мы положим x1>0 или x2>0, то значение ¦ увеличится. Но эти же коэффициенты с их знаками стоят в индексной строке.
Итак, мы приходим к следующему выводу: наличие в индексной строке отрицательных чисел при решении задачи на максимум свидетельствует о том, что нами оптимальное решение не получено, и то, что от табл. 5.3 надо перейти к следующей.
Переход к новой таблице, т.е. к новой улучшенной программе осуществляем следующим способом: в индексной строке находим наибольшее по абсолютному значению отрицательное (а при задаче на минимум - наибольшее положительное) число. В нашем примере этим числом будет - 4. Найденное число определяет ведущий или ключевой столбец. Затем мы делим свободные члены на положительные элементы ведущего столбца и выбираем из полученных отношений наименьшее. Наименьшее отношение определяет ведущую строку. В данном случае имеем:
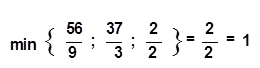
Таким образом, ведущей строкой будет строка A5. На пересечении ведущего столбца и ведущей строки стоит разрешающий элемент. В нашем случае - это число 2.
Теперь мы приступаем к составлению второй таблицы или второго плана. Вместо единичного вектора A5 мы в базис вводим вектор A2. Переход к новому базису, как это известно, эквивалентен элементарному преобразованию матрицы, элементами которой служат числа табл. 5.3. А именно: в новой таблице элемент строки, соответствующий элементу ведущей строки прежней таблицы, равен этому элементу ведущей строки, разделенному на разрешающий элемент. чтобы получить любой другой элемент новой симплексной таблицы, нужно от соответствующего элемента прежней таблицы отнять произведение элемента ведущей строки на элемент ведущего столбца, разделенное на разрешающий элемент. Например, элементу 4 (табл. 5.3) будет соответствовать элемент табл. 5.4:
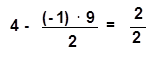
Таким образом, мы переходим ко второй таблице (таблица 5.4). Указанные выше преобразования относятся к столбцам B, A1, A2, A3, A4 , A5.
Таблица 5.4.
| Базисные | Коэффициенты | Вектор свободных | |||||
| векторы | линейной формы С | членов В | A1 | A2 | A3 | A4 | A5 |
| A3 | 17/2 | -9/2 | |||||
| A4 | 13/2 | -3/2 | |||||
| A5 | -1/2 | 1/2 | |||||
| Индексная строка ¦ j-Сj | -5 |
Из табл. 5.4 видно, что значение линейной формы возросло и теперь равно 4. Однако наличие в индексной строке отрицательных чисел свидетельствует о том, что это значение еще можно увеличить. Переходим к следующей симплексной таблице. число «5» определяет ведущий столбец. Находим ведущую строку. Для этого определяем:
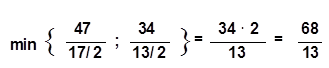
Итак, разрешающим элементом будет 13/2. Вектор A4 выводим из базиса и вводим вместо него вектор A1. Пересчет коэффициентов осуществляем по указанным выше правилам и получаем таблицу 5.5.
Таблица 5.5
| Базисные | Коэффициенты | Вектор свободных | |||||
| векторы | линейной формы С | членов В | A1 | A2 | A3 | A4 | A5 |
| A3 | 33/13 | -17/13 | -33/13 | ||||
| A1 | 68/13 | 2/13 | -3/13 | ||||
| A2 | 47/13 | 1/13 | 5/13 | ||||
| Индексная строка ¦ j-Сj | 392/13 | 10/13 | 11/13 |
В индексной строке нет отрицательных элементов. Следовательно, мы получим оптимальную программу. Оптимальное решение:
x1=68/13; x2=47/13; x3=33/13; x4 = x5 = 0.
Дата добавления: 2015-04-01; просмотров: 1053;
