Многокритериальная оптимизация
þ задачи, в которых оптимизацию проводят по нескольким параметрам, называют задачами многокритериальной или векторной оптимизации.
Как и при линейном программировании задачи многокритериальной оптимизации включают в себя три основные части.
три основные части задачи многокритериальной оптимизации:
Àцелевую функцию,
Áограничения,
Âграничные условия.
Наиболее часто целевая функция представляется обобщенными показателями эффективности, которые представляют собой взвешенную сумму частных показателей, в которую каждый из них входит с определенным весом, отражающим его важность:
W= a1 .w1 + a2 .w2 + ... + an .wn
Для тex показателей, которые желательно увеличить, веса берутся положительные, а для тex, которые желательно уменьшить - отрицательные.
Назначение коэффициентов весов проводят с помощью экспертных оценок. Методы экспертных оценок достаточно широко распространены. Математических методов определения экспертных оценок достаточно много. Рассмотрим некоторые из них.
Математические методы определения экспертных оценок:
À Непосредственное назначение коэффициентов весов.
Согласно этому методу каждый i-й эксперт для каждого k-ого параметра должен назначить коэффициент веса aik таким образом, чтобы сумма коэффициентов веса, назначенная одним экспертом для различных параметров, равнялась 1.

i=1, n, где n - число экспертов.
В качестве коэффициента веса k-ого параметра ak принимают среднее значение по результатам экспертизы всех экспертов:
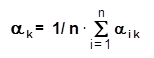
Á Oценка важности параметров в баллах. В этом случае каждый эксперт назначает каждому параметру оценку по десяти бальной системе. Наиболее важный параметр оценивается более высоким баллом. В результате экспертизы заполняется таблица, и находятся коэффициенты веса.
Дата добавления: 2015-04-01; просмотров: 861;
