Комбинаторная оптимизация и задача коммивояжера
В задачах комбинаторной оптимизации требуется найти наилучшее из конечного, но обычно очень большого числа возможных решений. Если задача характеризуется характерным числом элементов (размерностью задачи), то типичное число возможных решений, из которых предстоит сделать выбор, растет экспоненциально - как или еще скорее - как (напомним, что согласно известной формуле Стирлинга , для достаточно больших ).
Это свойство делает простой метод перебора всех вариантов, в принципе гарантирующий решение при конечном числе альтернатив, чрезвычайно неэффективным, т.к. такое решение требует экспоненциально большого времени. Эффективными же признаются решения, гарантирующие получение ответа за полиномиальное время, растущее как полином с ростом размерности задачи, т.е. как .[14]
1 Различие между полиномиальными и экспоненциальными алгоритмами восходит к фон Нейману (von Neumann, 1953)
Задачи, допускающие гарантированное нахождение оптимума целевой функции за полиномиальное время, образуют класс . Этот класс являюется подклассом более обширного класса задач, в которых за полиномиальное время можно всего лишь оценить значение целевой функции для конкретной конфигурации, что, естественно, гораздо проще, чем выбрать наилучшую из всех конфигураций. До сих пор в точности не известно, совпадают ли эти два класса, или нет. Эта проблема, , о которую сломано уже немало математических копий. Если бы эти классы совпадали, для любой задачи комбинаторной оптимизации, точное можно было бы гарантированно найти за полиномиальное время. В такой "подарок судьбы" никто не верит, и практически разрешимыми считаются задачи, допускающие полиномиальное решение хотя бы для типичных (а не наихудших) случаев. Такова, например, общая задача линейного программирования.
Для более трудных задач достаточно было бы и более слабого условия - нахождения субоптимальных решений, локальных минимумов целевой функции, не слишком сильно отличающихся от абсолютного минимума. Нейросетевые решения как раз и представляют собой параллельные алгоритмы, быстро находящие субоптимальные решения оптимизационных задач, минимизируя целевую функцию в процессе своего функционирования или обучения.
Самые трудные задачи класса называют -полными. Это название объясняется тем, что если бы удалось доказать, что существует полиномиальное решение такой задачи, то такое решение существовало бы и для любой другой задачи класса , т.е. классы и совпадали бы. Поскольку, как уже говорилось, такой сценарий крайне маловероятен, именно для таких проблем наиболее важен поиск субоптимальных решений.
Все -полные задачи одинаково сложны (поскольку все они сводятся друг к другу за полиномиальное время), и методы решения любой из них можно применять также и к другим задачам комбинаторной оптимизации. Поэтому нам в этой главе достаточно сосредоточиться на одной такой задаче. Исторически наиболее исследованной и популярной задачей такого рода (своего рода "мушкой дрозофилой" комбинаторной оптимизации), которая используется для сравнения различных алгоритмов, стала задача коммивояжера.
В классической постановке, коммивояжер должен объехать городов по замкнутому маршруту, посетив каждый из них лишь однажды, таким образом, чтобы полная длина его маршрута была минимальной. Если решать задачу коммивояжера “в лоб” - перебором всех замкнутых путей, связывающих городов, то придется проверить все возможных маршрутов. Будучи -полной, задача коммивояжера не имеет практически реализуемого точного решения. На примере этой задачи мы ниже и рассмотрим различные методы ее приближенного решения с помощью нейросетей.
Оптимизация и сеть Хопфилда
В 1985г. Хопфилд и Танк предложили использовать минимизирующие энергию нейронные сети для решения задач оптимизации (Hopfield & Tank, 1985). В качестве примера они, естественно, рассмотрели задачу коммивояжера.
Для решения этой задачи с помощью нейронной сети Хопфилда нужно закодировать маршрут активностью нейронов и так подобрать связи между ними, чтобы энергия сети оказалась связанной с полной длиной маршрута. Хопфилд и Танк предложили для этого следующий способ.
Рассмотрим сеть, состоящую из бинарных нейронов, состояния которых мы обозначим , где индекс кодирует город, а индекс - номер города в маршруте (см. Рисунок 32). Если обозначить через расстояние между -м и-м городами, решение задачи коммивояжера сводится к минимизации целевой функции
при дополнительных условиях
и ,
первое из которых говорит о том, что любой город в маршруте встречается лишь однажды, а второе - что маршрут проходит через каждый город.
Общий подход к ограничениям в задачах оптимизации состоит в том, что в итоговый функционал, подлежащий минимизации, включаются штрафные члены, увеличивающие целевую функцию при отклонении от накладываемых ограничений. В данном случае в качестве энергии состояния сети можно выбрать функционал
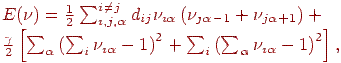
где т.н. множитель Лагранжа регулирует строгость соблюдения дополнительных условий в конечном решении.
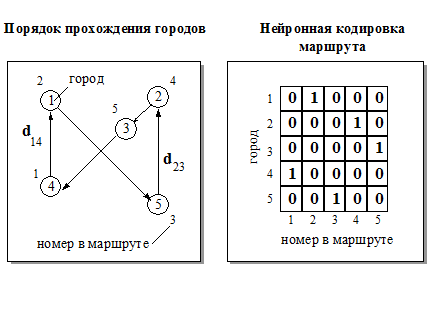
Рисунок 32. Слева - один из возможных маршрутов коммивояжера в случае задачи с 5 городами. Справа - кодировка этого маршрута состояниями 25 бинарных нейронов.
Осмысленному решению будет соответствовать стационарное состояние сети, в котором лишь N нейронов сети будут активными () и в каждом столбце и в каждой строке матрицы будет находиться один и только один единичный элемент.
Величина множителя Лагранжа регулирует “торг” между поиском маршрута минимальной протяженности и осмысленностью вида самого маршрута. Частное решение, соответствующее локальному минимуму функционала , может быть осмысленным (второе слагаемое обращаются на нем в ноль), но первое слагаемое (длина маршрута) для него, возможно будет слишком велико. Наоборот, длина маршрута может быть достаточно мала, но одно из оставшихся слагаемых будет ненулевым и маршрут окажется не интерпретируем или недостаточен (например, проходит не через все города).
После того, как минимизируемая целевая функция для задачи коммивояжера построена, можно определить, какие связи в нейронной сети Хопфилда следует выбрать, так чтобы функционал энергии состояния в ней совпал с этой функцией. Для этого достаточно приравнять выражение для к энергии рекуррентной сети:
.
Таким образом находятся значения синаптических связей в сети:
и значений порогов нейронов. Общее число весов в сети - порядка .
1 Сети Поттса. Значительного продвижения в эффективности нейросетевой оптимизации можно добиться, выбрав более сложный тип нейронов - т.н. Поттсовские нейронны - для более естественного представления условий задачи в терминах нейросети (Gilsen et al., 1989). Поттсовский нейроны принимают одно из N значений, что можно описать N-вектором , в котором единица помечает принимаемое им значение. Если при решении задачи коммивояжера сопоставить таким нейронам города, а их состояния соотнести с номером города в туре, то условие посещения города лишь однажды будет гарантировано автоматически.
После того как сеть построена, можно, стартуя со случайного начального состояния, проследить ее эволюцию к стационарной конфигурации, которая может дать если не оптимальное, то, по крайней мере, хорошее решение задачи. К сожалению, в описанном виде сеть чаще всего "застревает" в локальном минимуме относительно далеком от оптимума.
Для улучшения ситуации Хопфилд и Танк предложили использовать сети с непрерывными (аналоговыми) нейронами, принимающими любые значения в интервале .[15] В качестве тестовых они использовали задачи с 10 и 30 городами. В первом случае сеть в 20 попытках 16 раз эволюционировала к состояниям, описывающим осмысленный маршрут и в 10 случаях давала один из двух возможных оптимальных маршрутов. Поскольку для задачи с городами полное число всевозможных маршрутов равно (делитель 2N возникает вследствие инвариантности маршрута относительно циклического сдвига и обращения направления движения), то в задаче с 10 городами оно составляет 181440. Таким образом, выигрыш при использовании сети, по сравнению со случайным выбором составляет 105. В случае задачи с 30 городами полное число маршрутов приблизительно равно 4.4x1030. Экономия, даваемая сетью, составила в этом случае 1022. В дальнейшем было показано, что использование сети Кохонена дает лучшие результаты при решении той же задачи. Однако, поскольку на практике (в робототехнике, при проведении стыковки космических аппаратов, в автоматической навигации) необходимо быстро находить хорошее, но не обязательно лучшее решение, то при электронной реализации аналоговая сеть Хопфилда дает исключительно эффективное решение задач оптимизации.
В дальнейшем разные исследователи выявили и другие особенности описанного подхода. Было показано, что недостатком оригинальной схемы Хопфилда и Танка является то, что простейшая сеть Хопфилда имеет тенденцию включать в маршрут ближайшие друг к другу города. Это происходит из-за того, что в определяющую длину маршрута часть функции Ляпунова входят парные произведения состояний нейронов сети. В результате, с увеличением числа городов маршрут, предлагаемый сетью, как правило, распадается на локально оптимальные участки, соединение которых, однако, далеко от оптимального. Ситуацию можно улучшить, если стимулировать сеть находить, например, локально наилучшие тройки городов. Для этого основная часть функции Ляпунова может быть представлена в виде
.
Однако, сети, динамика которых направляется такой функцией Ляпунова, должны состоять из более сложных нейронов, нелинейно суммирующих внешние воздействия - нейронов высокого порядка (в данном случае - второго):
.
Купер показал, что использование таких сетей значительно улучшает результаты поиска оптимального решения. Так для такая сеть вдвое чаще находит оптимальное решение, чем обычная сеть Хопфилда. Повышение порядка сети приводит к дальнейшему увеличению улучшению найденных сетью решений.
Отметим в заключение, что мы упомянули только о небольшой части разработанных к настоящему времени способов улучшения свойств минимизирующих энергию нейронных сетей при решения задач оптимизации.
Имитация отжига
В предыдущем разделе мы заметили, что переход от бинарных нейронов к аналоговым значительно улучшил свойства решения. Аналогичного эффекта можно добиться используя по-прежнему бинарные нейроны, но заменив детерминистскую динамику стохастической, характеризуемой некоторой эффективной температурой . При этом среднее значение состояния нейрона также будет лежать в допустимом интервале .
Положительная роль температуры заключается в том, что шум позволяет системе покидать локальные минимумы энергии и двигаться в сторону более глубоких энергетических минимумов. Соответствующий (не нейросетевой) алгоритм оптимизации был предложен в 1953 г. и получил название имитации отжига (Metropolis et al., 1953). Этот термин происходит от названия способа выжигания дефектов в кристаллической решетке. Атомы, занимающие в ней неправильное место, при низкой температуре не могут сместиться в нужное положение - им не хватает кинетической энергии для преодоления потенциального барьера. При этом система в целом находится в состоянии локального энергетического минимума. Для выхода из него металл нагревают до высокой температуре, а затем медленно охлаждают, позволяя атомам занять правильные положения в решетке, соответствующее глобальному минимуму энергии.
Субоптимальное решение некоторой задачи оптимизации, например, задачи коммивояжера, также может рассматриваться как решение в котором имеются дефекты - неправильные части маршрута. Лин и Кернигэн (Lin & Kernigan, 1973) ввели элементарные операции изменения текущего решения, такие как перенос (часть маршрута вырезается и вставляется в другое место) и обращение (выбирается фрагмент маршрута и порядок прохождения городов в нем меняется на обратный). При применении одной из этих операций происходит изменение маршрута с на , и значение минимизируемого функционала меняется на . В соответствии с принципами термодинамики, это изменение принимается с вероятностью
где Т - эффективная температура. Таким образом в методе отжига с некоторой вероятностью допускается переход системы в состояния с более высокой энергией. Эта вероятность тем выше, чем выше эффективная температура. Поиск минимума начинается с некоторого начального маршрута при высоком значении температуры. По мере эволюции состояния системы эта температура медленно снижается (для примера - на 5% после осуществления элементарных операций изменения маршрута). Поиск продолжается до тех пор, пока система не захватывается энергетическим минимумом, из которого она уже не может выйти за счет тепловых флуктуаций. Многочисленные исследования показали, что метод имитации отжига является очень эффективным способом получения решений близких к оптимальному и часто служит эталоном сравнения для нейросетевых подходов. Заметим, однако, что при реализации “в железе” нейросетевой подход все равно оказывается вне конкуренции по скорости получения решения.
Метод эластичной сети
Иной подход к решению задачи коммивояжера использовали в 1987 году Дурбин и Уиллшоу (Durbin & Willshaw, 1987). Хотя они явно и не использовали в своей работе понятия искусственной нейронной сети, но в качестве отправной точки упоминали об аналогии с механизмами установления упорядоченных нейронных связей. Исследователи предложили рассматривать каждый из маршрутов коммивояжера как отображение окружности на плоскость, так что в каждый город на плоскости отображается некоторая точка этой окружности. При этом требуется, чтобы соседние точки на окружности отображались в точки, по возможности ближайшие и на плоскости. Алгоритм стартует с помещения на плоскость небольшой окружности (кольца), которая неравномерно расширяясь проходит практически около всех городов и, в конечном итоге, определяет искомый маршрут. Каждая точка расширяющегося кольца движется под действием двух сил: первая перемещает ее в сторону ближайшего города, а вторая смещает в сторону ее соседей на кольце так, чтобы уменьшить его длину. По мере расширения такой эластичной сети, каждый город оказывается ассоциирован с определенным участком кольца.
Вначале все города оказывают приблизительно одинаковое влияние на каждую точку маршрута. В последующем, большие расстояния становятся менее влиятельными, и каждый город становится более специфичным для ближайших к нему точек кольца. Такое постепенное увеличение специфичности, которое, конечно, напоминает уже знакомый нам метод обучения сети Кохонена, контролируется значением некоторого эффективного радиуса . Если обозначить через вектор, определяющий положение -го города на плоскости, а -координату -й точки на кольце, то закон изменения последний имеет вид
,
где параметры определяют относительное воздействие на точку описанных выше двух сил. Коэффициенты , определяющие воздействие -го города на -ю точку кольца, являются функцией расстояния и параметра . Эти коэффициенты нормированы так, что полное воздействие каждого из городов оказывается одинаковым:
,
где - положительная, ограниченная и убывающая функция d, приближающаяся к нулю при Если в качестве этой функции выбрать распределение Гаусса , то можно определить функцию Ляпунова
,
которая минимизируется в ходе динамического изменения параметров кольца.
Дурбин и Уиллшоу показали, что для задачи с 30 городами, рассмотренной Хопфилдом и Танком, метод эластичной сети генерирует наикратчайший маршрут примерно за 1000 итераций. Для 100 городов найденный этим методом маршрут лишь на 1% превосходил оптимальный.
Оптимизация с помощью сети Кохонена.
Успех применения метода эластичной сети для решении задачи коммивояжера был оценен Фаватой и Уолкером, понявшими, что в нем, по сути, используется отображение двумерного распределения городов на одномерный кольцевого маршрута (Favata & Walker, 1991). Поскольку в наиболее общем виде такой подход был сформулирован Кохоненом, то использование его самоорганизующихся карт для оптимизации оказалось вполне естественным. Сеть Кохонена позволяет обеспечить выполнение условия, которому должен удовлетворять хороший маршрут в задаче коммивояжера: близкие города на плоскости должны быть отображены на близкие в одномерном маршруте.
Алгоритм решения задачи следует из оригинальной схемы Кохонена, в которую вносятся лишь небольшие изменения. Используется сеть, состоящая из двух одномерных слоев нейронов (т.е. содержащая лишь один слой синаптических весов). Входной слой состоит из трех нейронов, а выходной - из N (по числу городов). Каждый нейрон входного слоя связан с каждым выходным нейроном. Все связи вначале инициируются случайными значениями. Для каждого города входной 3-мерный вектор формируется из двух его координат на плоскости, а третья компонента вектора представляет из себя нормирующий параметр, вычисляемый так, чтобы все входные вектора имели одинаковую Евклидову длину и никакие два вектора не были бы коллинеарны. Это эквивалентно рассмотрению двумерных координат городов, как проекций трехмерных векторов, лежащих на сфере. Обозначим через 3-мерный вектор синаптических связей, связывающих j-й выходной нейрон с входными нейронами. Если - трехмерный входной вектор, определяющий i -й город, то активация j-го выходного нейрона при подаче на вход определяется скалярным произведением (,). Выходной нейрон, для которого это произведение максимально, называется образом города.
Алгоритм формирования маршрута формулируется следующим образом. Выбираются значения для параметра усиления и радиуса взаимодействия r. Следующий цикл выполняется вплоть до выполнения условия .
1) Выбирается случайный город с.
2) Определяется номер образа города в выходном слое - .
3) Векторы связей , соединяющих нейрон , и всех его 2r близлежащих соседей справа и слева: j = - r, - r +1, ..., , ..., + r - 1, + r модифицируются следующим образом:
,
где - Евклидова норма вектора . Для устранения концевых эффектов слой выходных нейронов считается кольцевым, так что N-й нейрон примыкает к первому.
4) Радиус взаимодействия постепенно уменьшается согласно некоторому правилу (например, вначале можно положить , затем за первые 10% циклов снизить его до значения 1, которое далее поддерживается постоянным).
5) Параметр усиления постепенно снижается на небольшую величину ( например, в экспериментах Фавата и Уолкера он линейно уменьшался до нуля).
Конкретный вид законов изменения радиуса взаимодействия и параметра усиления, как правило, не имеет большого значения.
После завершения процесса обучения, положение города в маршруте определится положением его образа в кольцевом выходном слое. Иногда случается, что два или большее число городов отображаются на один и тот же выходной нейрон. Подобная ситуация может интерпретироваться так, что локальное упорядочивание этих городов не имеет значения и требует только локальной оптимизации части маршрута. При нескольких десятках городов такая оптимизация может скорректировать его длину на величину до 25%. Для сотен городов она, как правило, не улучшает результат и поэтому не используется.
Эксперименты Фаваты и Уолкера, проведенные для задачи коммивояжера с 30 городами дали лучшие результаты, чем полученные с помощью сети Хопфилда (см. таблицу).
Таблица 9. Сравнение результатов решения задачи коммивояжера с 30 городами
| сеть Хопфилда | сеть Кохонена | |
| Длина маршрута | < 7 | < 5.73 |
| Средняя длина маршрута | > 6 | 4.77 |
| Наименьшая длина маршрута | 5.07 | 4.26 |
Однако для большего числа городов сеть Кохонена все же в среднем дает более длинные маршруты, чем метод имитации отжига (примерно на 5%). При практическом применении нейросетевых подходов к решению задач оптимизации, однако, главное значение имеет не столько близость решения к глобальному оптимуму, сколько эффективность его получения. В этом смысле сеть Кохонена значительно эффективнее имитации отжига. Однако, и ее использование, как и в случае использования других лучших методов оптимизации, требует вычислительных затрат, растущих не медленне, чем . Ниже мы опишем нейросетевой подход, в котором они растут линейно с размерностьюзадачи.
Растущие нейронные сети
Эффективное практическое применение нейронных сетей для оптимизации возможно, если вычислительные затраты у соответствующей модели не слишком быстро растут с ростом размерности задачи. Так, для задачи коммивояжера затраты при эмуляции сети Хопфилда на последовательном компьютере растут как , т.к. каждый из нейронов имеет порядка синаптических весов. Эвристический подход Лина и Кернигана масштабирует вычислительные затраты как . Фритцке и Вильке предложили нейросетевую систему очень близкую к сети Кохонена, для которой затраты даже при ее эмуляции на последовательном компьютере растут лишь линейно с размерностью задачи (Fritzke & Wilke, 1991).
Предложенная ими модель относится к классу растущих нейронных сетей. Такие сети по-своему решают задачу адаптации своей структуры к требованиям решаемой задачи. Вспомним многослойные персептроны, для которых количества скрытых слоев и нейронов в них часто выбираются методом проб и ошибок. Как уже отмечалось в связи с этим, имеются два подхода к адаптивному выбору архитектуры нейросетей. В первом подходе заведомо избыточная нейросеть прореживается до нужной степени сложности. Растущие сети, напротив, стартуют с очень простых и небольших структур, которые разрастаются и усложняются по мере необходимости.
Фритцке и Вильке разработали целый класс самоорганизующихся (и обучаемых с учителем) сетей с изменяющейся структурой, такие как Растущие Клеточные Структуры, Растущий Нейронный Газ и Растущие Сетки. Первые и были использованы ими для решения задачи коммивояжера (и других задач комбинаторной оптимизации).
Растущая клеточная структура для задачи коммивояжера представляет из себя вначале кольцо из трех ячеек нейронов. Каждый нейрон характеризуется двумерным вектором , определяющим его положение на плоскости. Каждому нейрону в кольце приписывается также своя величина погрешности , которая вначале полагается равной нулю. Дальнейшая последовательность действий включает две следующие основные элементарные операции: смещение и добавление нового нейрона.
Смещение(см. Рисунок 33)
· выбирается случайный город с
· определяется нейрон-победитель , ближайший к этому городу
· положение нейрона и его двух ближайших в кольце соседей смещается в сторону города с на определенную долю расстояния до него.
Эти операции очень близки к используемым в модели Кохонена. Различие состоит в том, что в последней радиус, в котором определяется соседство и параметр адаптации уменьшаются со временем.
Рисунок 33. Процедура смещения перемещает нейрон-победитель и его ближайших соседей в сторону случайно выбранного города
Добавление нового нейрона.
Со временем после нескольких циклов смещений накапливается информация, на основании которой принимается решение о месте, в котором должен быть добавлен новый нейрон. Каждый раз, когда для случайно выбранного города определяется ближайший к нему нейрон , локальная ошибка для последнего получает приращение. Большое значение этой ошибки служит указанием на то, что соответствующий нейрон лежит в области, где отношение <число нейронов>/<число городов> невелико. Именно в таких областях следует добавлять новые нейроны, поскольку для получения правильного осмысленного маршрута около каждого города должен находиться свой ближайший нейрон. Маршрут и определяется путем перехода вдоль кольца к нейрону, являющимся ближайшим к некоторому городу. Алгоритм поиска оптимального маршрута, использующий две описанные операции, формулируется следующим образом
0) Инициализация: генерируется кольцевая структура, состоящая из трех нейронов, имеющих случайное положение на плоскости.
1) Осуществляется фиксированное число шагов распространения. На каждом шаге пересчитывается значение локальной ошибки .
2) Определяется “наихудшее” звено в кольце, связывающее два нейрона и , для которых сумма максимально. Новый нейрон вставляется в середину звена связывающего нейроны и , и его ошибка инициализируется величиной . В то же время значения ошибок для нейронов и уменьшается таким образом, чтобы суммарная ошибка сохранилась: ,
3) Если для любых двух городов ближайшие к ним нейроны различны между собой, то маршрут найден. В противоположном случае возвращаемся к шагу 1.
Очевидно, что решение задачи может быть найдено не ранее того, как число нейронов в кольце достигнет числа городов . В действительности для его достижения требуется сеть с 2N-3N нейронами. Исходя из этого эмпирического наблюдения, согласно которому число итераций имеет порядок , можно оценить общую сложность алгоритма. На шаге 1 требуется инспекция всех нейронов для поиска ближайшего к данному городу. Она производится раз и, поскольку это число постоянно, полное число инспекций также имеет порядок . На шаге 2 необходимо проверить каждое звено цепи, чтобы найти то, которому соответствует максимальная суммарная ошибка концевых нейронов. Поскольку число звеньев равно числу нейронов, то число действий опять имеет порядок . На шаге 3 для каждого города необходимо найти ближайший нейрон, что, как минимум, требует действий. Таким образом, так как шаги 1-3 требуют по меньшей мере операций, а цикл повторяется раз, то временная сложность алгоритма как минимум равна . Пространственная сложность алгоритма составляет , так как необходимо резервировать память для N городов, нейронов и некоторых локальных переменных.
Для улучшения квадратичной временной сложности описанного алгоритма Фритцке и Вильке модифицировали шаги 1-3. Они учли, что согласно численным экспериментам вначале кольцевая структура нейронов быстро распределяется по всей области размещения городов, и затем с ростом числа нейронов изменения приобретают локальный характер. Такое поведение натолкнуло их на идею заменить глобальный поиск нейрона-победителя на шаге 1 приближенной локальной процедурой. А именно: для каждого города запоминается тот нейрон, который наиболее часто оказывался к нему ближайшим, и если город выбран вновь, то поиск ближайшего к нему нейрона ограничивается этим нейрономи его ближайшими по кольцу соседями вплоть до порядка k. Поскольку k есть константа, то сложность поиска оказывается в этом случае .

Рисунок 34. Локальный поиск наилучшего нейрона: -предыдущий нейрон ; ближайшие его соседи вплоть до 2 порядка являются кандидатами в победители на следующем шаге.
Для устранения на шаге 2 линейного поиска звена с максимальной ошибкой используется тот факт, что таким звеном является то, которое связывает нейроны, часто становящиеся победитями.
Третий шаг тоже можно модифицировать: если некоторый нейрон несколько раз оказывается ближайшим для данного города, значит для этого города структура кольца уже стабилизировалась и нейрон “приклеивается” к данному пункту маршрута. Это означает, что он совмещается со своим городом и больше уже не двигается. Город же удаляется из списка городов, разыгрываемых на шаге распределения. Когда этот список становится пустым процесс поиска маршрута заканчивается.
Таким образом, каждый шаг в цикле теперь требует постоянное число операций и временная сложность всего алгоритма становится порядка .
Описанный эффективный нейросетевой подход (FLEXMAP) был протестирован на разных распределениях городов числом до 200 и неизменно находил маршруты, отличающиеся не более чем на 9% от оптимального.
Нейросетевая оптимизация и другие “биологические “методы
Преимущества и недостатки нейросетевой оптимизации познаются в сравнении с другими развитыми в настоящее время методами. Из методов, которые иногда дают аналогичные, а порой и лучшие результаты, отметим генетические и эволюционные алгоритмы (Fogel, 1993), а также метод муравьиных колоний (Dorigo & Gambardella, 1996).
В этом разделе мы очень кратко остановимся на них, поскольку эти подходы, так же как и нейросети, используют ясные и плодотворные биологические аналогии. Кроме того, генетические алгоритмы широко используются и для обучения нейронных сетей самих по себе, поскольку обучение нейросетей связано с минимизацией функционала ошибки.
Дата добавления: 2015-04-10; просмотров: 4194;
