Метод муравьиных колоний
Энтомологи установили, что муравьи способны быстро находить кратчайший путь от муравейника к источнику пищи. Более того, они могут адаптироваться к изменяющимся условиям, находя новый кратчайший путь. Рассмотрим Рисунок 36: муравьи движутся по прямой, соединяющей муравейник с местом, в котором находится пища. При движении муравей метит свой путь специальными веществами - феромонами, и эта информация используется другими муравьями для выбора пути. А именно, муравьи предпочитают тропки наиболее обогащенные феромонами. Это элементарное правило поведения муравьев и определяет их способность находить новые пути, если старый оказывается перерезанным преградой. Действительно, достигнув этой преграды, муравьи уже не смогут продолжить свой путь и с равной вероятностью будут обходить ее справа и слева. То же самое будет происходить и на обратной стороне преграды. Однако, те муравьи, которые случайно выберут кратчайший путь (налево от преграды и направо - на обратном пути), будут быстрее проходить свой путь и он с большей скоростью станет обогащаться феромонами. Поэтому следующие муравьи будут предпочитать именно этот наикратчайший путь, метя его и далее. Очевидная положительная обратная связь быстро приведет к тому, что кратчайший путь станет единственным маршрутом движения насекомых.

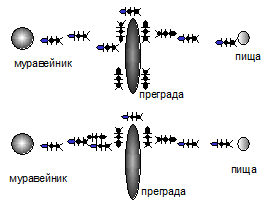
Рисунок 36. Муравьи находят новый кратчайший новый путь (сверху от преграды) который быстрее обогащается феромонами.
Подобный процесс может осуществляться и в компьютерном мире, населенном Искусственными Муравьями (ИМ). Такие муравьи могут решить и нашу задачу коммивояжера. В этом случае они движутся от города к городу по ребрам соответствующего графа. При этом они выбирают направление движения, используя вероятностную функцию, зависящую как от предыдущих попыток движения по данному ребру, так и от эвристического значения, являющегося функцией длины ребра. ИМ с большей вероятностью будут предпочитать ближайшие города и города, связанные ребрами, наиболее богатыми феромонами. Первоначально искусственных муравьев размещаются в случайно выбранных городах. В каждый последующий момент времени они перемещаются в соседние города и изменяют концентрацию феромона на своем пути (локальная модификация). После того, как все ИМ завершат движения по замкнутому маршруту, тот из них, который проделал кратчайший путь, добавляет к его звеньям количество феромона, обратно пропорциональное длине этого пути (глобальная модификация). В отличие от живых муравьев, ИМ обладают способностью определять расстояние до соседних городов и помнят, какие города они уже посетили. Оказывается, метод искусственных муравьиных колоний может давать результаты, лучшие чем при использовании имитации отжига, нейронных сетей, и генетических алгоритмов.
Таблица 10. Результаты решения задачи коммивояжера (длина маршрута)
| Набор | Муравьи | Отжиг | Эластич. Сети | Сети Кохонена |
| 5.86 | 5.88 | 5.98 | 6.06 | |
| 6.05 | 6.01 | 6.03 | 6.25 | |
| 5.57 | 5.65 | 5.70 | 5.83 | |
| 5.70 | 5.81 | 5.86 | 5.87 | |
| 6.17 | 6.33 | 6.49 | 6.70 |
Напомним вновь, что при электронной или оптической реализации нейросетевой подход находится вне конкуренции в ситуациях, когда необходимо очень быстро находить не обязательно оптимальное, но достаточно хорошее решение.
Кук, С. (1982) “Обзор вычислительной сложности”. Тьюринговская лекция в: Лекции лауреатов премии Тьюринга за первые двадцать лет 1966-1985. Мир. М:1993.
Burke, L.,L.., and Ignizio, J,P. (1992) “Neural networks and operations research: An overview”. Computers and Operations Research, 19, 179.
Cichocki, A. and Unbehauen, R. Neural Networks for Optimization and Signal Processing. John Wiley & Sons, 1994.
Cooper, B.,S. (1995) “Higher order neural networks - can they help us optimise?” Proceedings of the Sixth Australian Conference on Neural Networks (ACNN’95) , 29.
Cooper, B.S. (1996) “A comparison of the number of stable points of oprimisation networks”. Univ. of Adelaide, Report CSSIP TR, 4/96.
Dorigo, M., and Gambardella, L.,M. “Ant colonies for the traveling salesman problem”. Technical Report, Universte Libre de Bruxelles - TR/IRIDIA/1996-3.
Durbin, R., and Willshaw, D.(1987) “An analogue approach to the travelling salesman problem using an elastic net method”. Nature, 326, 689.
Favata, F. and Walker, R. (1991) “A study of the application of Kohonen-type neural network to the travelling salesman problem”. Biological cybernetics, 64, 463.
Fritzke, B. and Wilke, P.(1991) “FLEXMAP - A neural network for the travelling salesman problem with linear time and space complexity”. Proceddings of IJCNN-91, Singapore, 929.
Fogel, D. (1993) “Applying evolutionary programming to selected traveling salesman problems”. Cybernetics and Systems. An International Journal, 24, 27.
Gee, A.,H. (1993) Problem solving with optimization networks, PhD thesis, University of Cambridge.
Gislen, L., Soderberg, B., and Peterson, C. (1992) “Complex scheduling with Potts neural networks”, Neural Computation,4, 805.
Gislen,L., Soderberg, B., and Peterson, C. (1989) “Teachers and classes with neural networks”, International Journal of Neural Systems, 1, 167.
Hopfield J.,J., & Tank, D.,W. (1985) “Neural computation of decisions in optimization problems”, Biological Cybernetics, 52, 141.
Lin, S. & Kernigan, B.,W. (1973) “An effective heuristic algorithm for the travelling-salesman problem”, Operations Research, 21, 498.
Looi, C. (1992) “Neural networks methods in combinatorial optimization”, Computers and Operations Research, 19, 191.
Metropolis, N., Rosenbluth, A.,W., Rosenbluth, M.,N., Teller,A.,H., Teller, E.,J. (1953) J.Chem.Phys. 21, 1087.
von Neumann, J. (1953) “A certain zero-sum two-person game equivalent to the optimal assignment problem”. Contributions to the Theory of Games II.H.W. Kahn and A.W. Tucker, Eds. Princeton Univ. Press, Princeton, NJ.
Ogier, R.,G. and Beyer, D.,A. (1990) “Neural network solution to the link scheduling problem using convex relaxation”. Proceedings of the 1990 IEEE Global Telecommunications Conference, Dec.,1371.
Ohlsson,M., Peterson, C., and Soderberg, B. (1993) “Neural networks for optimization problems with inequality constraints - the knapsack problem”. Neural Computation, 5, 331.
Peterson, G. and Soderberg, B. (1989) “A new method for mapping optimization problems onto neural networks”, International Journal of Neural Systems, 1, 3.
Potvin, J-Y. (1993) “The travelling salesman problem - A neural network perspective”. ORSA Journal of Computing, 5, 328.
Smith, K., Palaniswami. M., and Krishnamoorthy, M. (1996) “Traditional heuristic versus Hopfield neural network approaches to car sequencing problem”. European Journal of Operational Research.
Vaithyanathan, S., and Ignizio, J.,P. (1992) “A stochastic neural network for resource constrained scheduling”. Computers and Operations Research, 19, 241.
Wilson, G.,V. and Pawley, G.,S. (1988) “On the stability of the Travelling Salesman Problem algorithm of Hopfield and Tank”. Biological Cybernetics, 58, 63.
Предобработка данных
Как решаются конкретные задачи? Кодирование входов-выходов. Виды нормировки. Линейная предобработка входов. Понижение размерности и отбор наиболее значимых входов.
& Вытапливай воск, но сохраняй мед.
Козьма Прутков
& Мелочи не играют решающей роли. Они решают все.
Х.Маккей. Как уцелеть среди акул
Дата добавления: 2015-04-10; просмотров: 1494;
