Неравенство Чебышева для доли или частости (неравенство Бернулли).

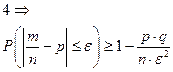Применим неравенство 4 для случайной величины →

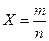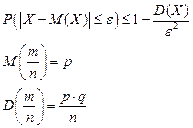
(7)

Замечание:

По неравенству 7 можно оценить либо вероятность P, либо отклонение ε, либо число испытаний n (см. аналогичные задачи 2-е следствие из интегральной теоремы Муавра-Лапласа).

Пример:

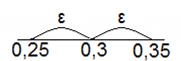Вероятность попадания в цель при одном выстреле равна 0,3. произведено 100 выстрелов. Оценить вероятность того, что процент попадания будет заключен в пределах от 25% до 35%. Уточнить результат с помощью следствия из интегральной теоремы Муавра-Лапласа.

Дано:

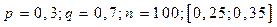
Используя формулу 7 →

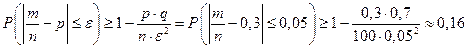
Ответ:

С вероятностью не менее, чем 0,16 можно утверждать, что процент попадания будет заключен в пределах от 25% до 35%.

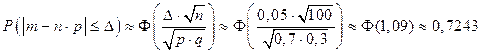
Вывод: полученный результат не противоречит, а уточняет предыдущую оценку.

Пример:

В условиях предыдущей задачи оценить количество выстрелов, чтобы с вероятностью не меньше чем 0,8 можно было гарантировать отклонение ε = 0,05.

Дано:

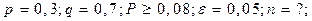
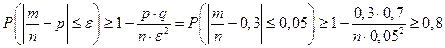
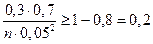
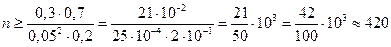
Ответ: Нужно произвести не менее 420 выстрелов, чтобы с вероятностью не менее 0,8 гарантировать отклонение ε = 0,05.