Неравенство Чебышева для симметричного интервала.

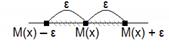Пусть случайная величина Х имеет математическое ожидание и дисперсию (М(х) и D(х)). Рассмотрим интервал, симметричный относительно математического ожидания.

Тогда справедливо следующее неравенство:

(3)

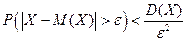
(4) 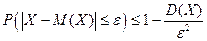, (самое распространенное)

Доказательство неравенства 4.

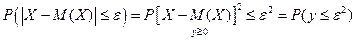применим к неотрицательной случайной величине y неравенство Маркова (формула 2) →

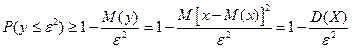
Пример:

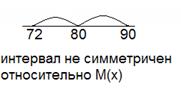Пусть случайная величина Х – число попаданий при 100 выстрелах. Вероятность попадания при каждом выстреле равна 0,8. Можно ли применить неравенство Чебышева для оценки вероятности того, что число попаданий заключено в границах от 72 до 90? Как рекомендуется изменить правую границу? После применения неравенства Чебышева уточнить результат с помощью следствия из интегральной теоремы Муавра-Лапласа.

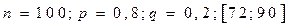
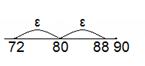
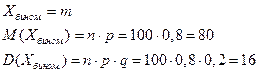
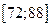
Используя формулу 4 →

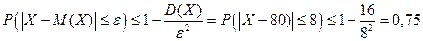
Ответ: С вероятностью не менее, чем 0,75 можно утверждать, что число попаданий заключено в интервале от 72 до 88.

Уточним результат с помощью 1-го следствия из интегральной теоремы Муавра-Лапласа для числа успехов в симметричном интервале:

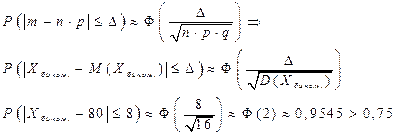
Вывод: полученный результат не противоречит, а уточняет предыдущую оценку.