Неравенство Чебышева для среднего арифметического случайных величин.

Пусть даны независимые случайные величины X₁, Х₂, …, Х_n имеющих математические ожидания a₁, a₂, …, a_n и дисперсии, каждая из которых ограничена числом С 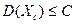, тогда справедливо неравенство:

(5)

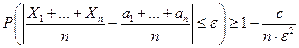
Пояснение к доказательству: неравенство 4 применяется к среднему арифметическому случайных величин. Тогда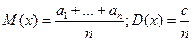

Пример:

Имеется 100 участков, засеянных пшеницей. Рассмотрим случайные величины X₁, Х₂, …, Х₁₀₀ – урожайность с каждого участка. Средняя урожайность на каждом участке составляет 40 центнеров с гектара. А средние квадратические отклонения этих случайных величин не превосходят 2-х центнеров. Оценить вероятность того, что средняя урожайность со всех участков отличается от средней на каждом участке не более чем на 3 единицы.

Дано:

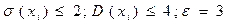X₁, Х₂, …, Х₁₀₀ – случайные величины.

a₁ = a₂ = …, a_n = 40

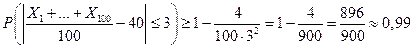
Ответ: С вероятностью не менее чем 0,99, можно утверждать, что средняя урожайность со всех участков отличается от средней на каждом участке не более чем на 3 единицы.