Нормально-распределенная случайная величина (закон Гаусса).

Определение: Случайная величина называется нормально-распределенной, если ее плотность вероятности имеет вид:

(5)

Замечание: нормальный закон распределения зависит от двух параметров: a, σ (σ²) (N(a;σ)).

Можно доказать, что математическое ожидание Х_N равно a.

(6)

Пример:

Написать плотность вероятности

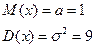
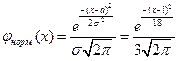
Функция распределения непрерывной случайной величины является первообразной от плотности и имеет вид:

(7) , где Φ(t) – интегральная функция Муавра-Лапласа.

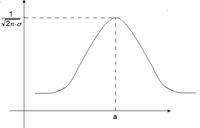
Замечание: т.к. Φ(t) – затабулирована, то для нормального закона распределения, можно вычислить любые вероятности. Графиком плотности вероятности нормального закона распределения является кривая Гаусса.

Замечания:

1. график симметричен относительно прямой х = а (математическое ожидание);

2. чем больше дисперсия σ², тем ниже max и тем шире пик кривой, т.е. ее разброс, относительно среднего значения.