НЕРАВЕНСТВА ЧЕБЫШЕВА

Теорема. Для любой случайной величины X с m_x, D_x выполняется следующее неравенство 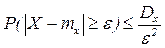где e>0.

Доказательство:

1. Пусть величина Х – ДСВ. Изобразим значения Х и М_х в виде точек на числовой оси Ох

0 х₁ А М_х В

Вычислим вероятность того, что при некотором 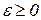величина Х отклонится от своего МО не меньше чем на ε:

.

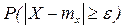Это событие заключается в том, что точка Х не попадет на отрезок [m_x-ε, m_x+ε], т.е.

--

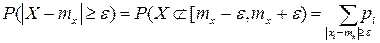для тех значений x, которые лежат вне отрезка [m_x-ε, m_x+ε].

Рассмотрим дисперсию с.в. Х:

.

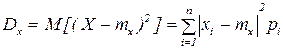Т.к. все слагаемые – положительные числа, то если убрать слагаемые, соответствующую отрезку [m_x-ε, m_x+ε], то можно записать:

,

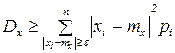т.к. 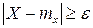, то неравенство можно усилить

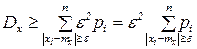
Þ 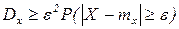Þ

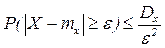
2. Для НСВ:

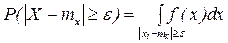
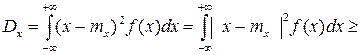
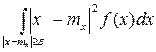- это интегрирование по внешней части отрезка [m_x-ε, m_x+ε].

Применяя неравенство 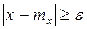и подставляя его под знак интеграла, получаем

.

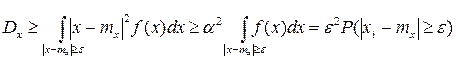Откуда и вытекает неравенство Чебышева для НСВ.

Следствие. 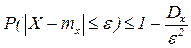- это 2-е неравенство Чебышева.

Доказательство: События 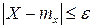и 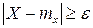- противоположны Þ .

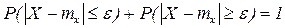1. Лемма:Пусть Х –СВ, e>0 – любое число. Тогда

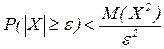
Доказательство:

,

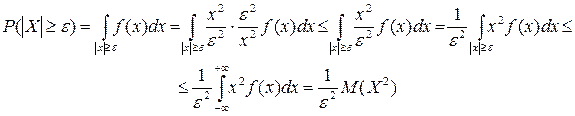Т.к. .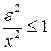

Следствие. .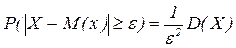

Д-во: Полагаем, вместо св Х – св Х-М(Х), т.к. М( Х-М(Х))²⁼D(X) и получаем неp-во.

Следствие: (правило трех сигм для произвольного распределения):

Полагаем в неравенстве Чебышева 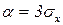, имеем

.

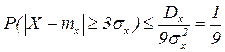Т.е. вероятность того, что отклонение св от ее МО выйдет за пределы трех СКО, не больше 1/9.

Неравенство Чебышева дает только верхнюю границ вероятности данного отклонения. Выше этой границы - значение не может быть ни при никаком распределении.