Первая теорема Чебышева.
Теорема. При достаточно большом числе независимых опытов среднее арифметическое значений случайной величины сходится по вероятности к ее математическому ожиданию:
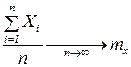
Доказательство: Рассмотрим величину Y равную
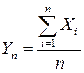 .
.
Определим числовые характеристики Yn my и DY.
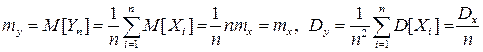
Запишем неравенство Чебышева для величины Yn
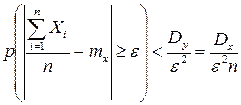
Как бы ни было мало число e, можно взять n таким большим, чтобы выполнялось неравенство 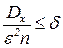 , где
, где 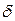 - сколь угодно малое число. Тогда
- сколь угодно малое число. Тогда
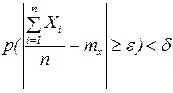 .
.
Переходя к противоположному событию:
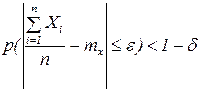
Т.е. вероятность может быть сколь угодно близкой к 1.
1.4.2. Вторая теорема Чебышева:
Теорема. Если Х1.....Хn – последовательность попарно независимых СВ с МО mx1....mxn и дисперсиями Dx1..Dxn ограничены одним и тем же числом Dxi<L (i=1..n ) , L=const, тогда для любого e, d>0 – бесконечно малых
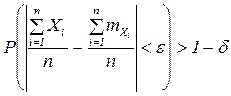 или
или 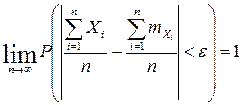
Доказательство: Рассмотрим СВ
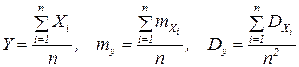 .
.
Применим к Y неравенство Чебышева:
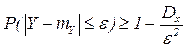 или
или 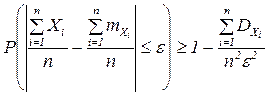
Заменим:
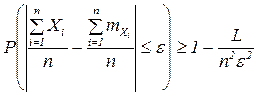
Как бы ни было мало число e, можно взять n таким большим, чтобы выполнялось неравенство 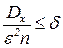 , где
, где 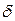 - сколь угодно малое.
- сколь угодно малое.
Т.е., взяв предел при n®¥ от обеих частей и 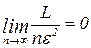 получаем:
получаем:
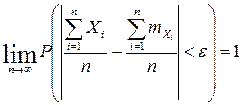
(так как вероятность не может быть больше 1).
Пример1.1. Производится большое число n независимых опытов, в каждом из которых некоторая случайная величина имеет равномерное распределение на участке [1,2]. Рассматривается среднее арифметическое наблюденных значений случайной величины X. На основании Закона больших чисел выяснить, к какому числу а будет приближаться величина Y при n→∞. Оценить максимальную практически возможную ошибку равенства Y≈a.
Решение. 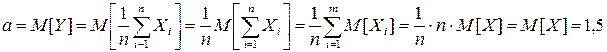 .
.
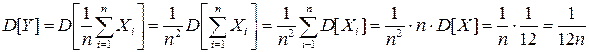 .
.
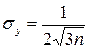 .
.
Максимальное практически возможное значение ошибки 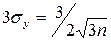 .
.
Дата добавления: 2015-05-05; просмотров: 1099;
