Выборочный метод.

Определение: Пусть требуется изучить признак Х. Все элементы подлежащие изучению называются генеральной совокупностью.

Обозначение: N – количество элементов генеральной совокупности (объем генеральной совокупности).

На всей генеральной совокупности признак Х имеет следующий вариационный ряд.

таблица 1.

		…
		…

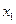
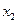
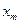
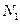
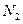
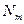
Вариационный ряд для всей генеральной совокупности называется генеральным вариационным рядом.

Характеристики генерального вариационного ряда называются генеральными характеристиками.

1. Генеральное среднее:

(1)

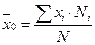
2. Генеральная дисперсия:

(2)

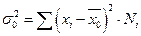
3. Генеральное среднее квадратическое отклонение:

(3)

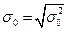
4. Генеральная доля или вероятность признака:

(4)

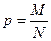
Как правило, распределение признака Х во всей генеральной совокупности неизвестно, т.е. неизвестен генеральный вариационный ряд, неизвестны все генеральные характеристики (формула 1-4).

Неизвестные параметры генеральной совокупности можно оценить с помощью результатов случайной выборки. Обследование всей генеральной совокупности бывает либо слишком дорого, либо практически невозможно (разрушаются элементы генеральной совокупности).

Определение: Часть элементов генеральной совокупности отобранных случайно называются случайной выборкой.

Количество элементов в выборке называется объемом выборки.

Выборка должна обладать свойством репрезентативности, т.е. она должна представлять всю генеральную совокупность. Для этого выборка должна отвечать следующим требованиям:

1. Выборка должна быть достаточно большой, чтобы проявились массовые закономерности.

2. Выборка должна быть случайной, чтобы каждый элемент генеральной совокупности мог иметь одинаковый с другими шанс попасть в выборку.

Существуют различные способы образования выборки (см. учебник).

Математическая статистика рассматривает собственно случайную выборку с повторным и бесповторным отбором членов. При повторном отборе элемент после обследования возвращается в генеральную совокупность, при бесповторном не возвращается. Бесповторная выборка более информативна, т.к. один и тот же элемент не может попасть в выборку дважды.

Пусть образована выборка объема n. В результате изучения признака Х на этой выборке получаем вариационный ряд, который называется выборочным вариационным рядом.

таблица 2.

		…
		…

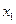
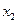
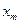
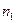
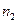
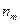
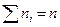
Все характеристики выборочного вариационного ряда называются выборочными характеристиками:

1. Выборочное среднее:

(5)

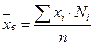
2. Выборочная дисперсия:

(6)

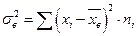
3. Выборочная средняя квадратическая ошибка:

(7)

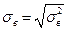
4. Выборочная доля или частость:

(8)

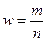
Все характеристики выборочного вариационного ряда являются случайными величинами, т.к. отобраны случайным образом.