Требования к оценкам.

Пусть случайная величина Х является оценкой неизвестного параметра θ:

1. Оценка называется несмещенной, если математическое ожидание оценки совпадает с оцениваемыми параметрами, т.е.:

(13)

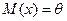
2. Оценка называется состоятельной, если при достаточно большом объеме выборки n практически достоверно, что оценка сколь угодно мало отличается от оцениваемого параметра.

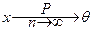
3. Состоятельная оценка называется эффективной, если она имеет наименьшую дисперсию на всех выборках данного объема n.

Теорема 3 (для средней):Выборочная средняя 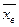является несмещенной состоятельной оценкой для генеральной средней: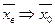

Теорема 4 (для доли):Выборочная доля является несмещенной состоятельной оценкой для генеральной доли: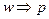

Теорема 5 (для дисперсии): Выборочная дисперсия является смещенной состоятельной оценкой для генеральной дисперсии: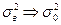

Несмещенной состоятельной оценкой для генеральной дисперсии является та называемая "исправленная" выборочная дисперсия:

(14)

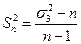
Замечание: при достаточно большом объеме выборки n множитель 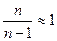, поэтому 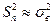, поэтому для практических целей можно применять любую из этих двух величин.