Определение выборочных статистических характеристик

Значения средних и рассеяния, определенные для выборки и для генеральной совокупности, могут отличаться. Это отличие трактуется как ошибка в определении параметров генеральной совокупности по параметрам выборки. Ошибка складывается из двух частей. Первая – это систематическая ошибка, зависящая от репрезентативности выборки, вторая – случайная ошибка, зависящая от объема выборки.

Любая репрезентативная выборка не полностью описывает поведение соответствующей генеральной совокупности. Поэтому любые статистические характеристики могут быть вычислены только приблизительны. В статистике такие приблизительные вычисления статистических характеристик называются оценками.

Оценка a*(x₁, x₂, ..., x_N) называется несмещенной, если ее математическое ожидание при любом объеме выборки N равно величине a, оцениваемой по генеральной совокупности.

Оценки начальных и центральных моментов:

,

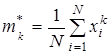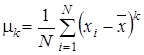
Пусть случайная величина X – выборка объема N со значениями: x₁, x₂, ..., x_N. Упорядоченная по возрастанию выборка x¹, x², ..., x^N, где x¹≤x²≤...≤x^N, называется вариационным рядом.

Размах варьирования случайной величины, размах выборки – разность между максимальным и минимальным элементами выборки L= x^N-x¹.

Гистограмма – это представление случайной величины в виде столбчатого графика, отражающего долю (количество) попаданий случайной величины в различные диапазоны ее значения. Гистограмма характеризуется минимальным и максимальным значениями случайной величины, размахом варьирования и модой.

Модальное значение случайной величины (мода) – это такое значение на гистограмме, которое соответствует середине диапазона с наибольшей высотой (наиболее вероятное значение).

Медианное значение случайной величины – это одно из ее значений в выборке, относительно которого одна половина значений превышает медианное, а другая половина не превышает ее.

На рисунке показан пример эмпирического асимметричного распределения и соответствующего ему теоретического распределения.

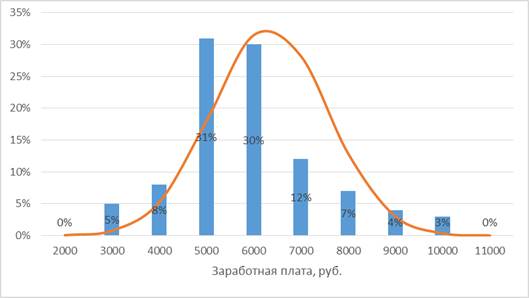
Распределение показателей рынка недвижимости могут иметь экспоненциальный характер.

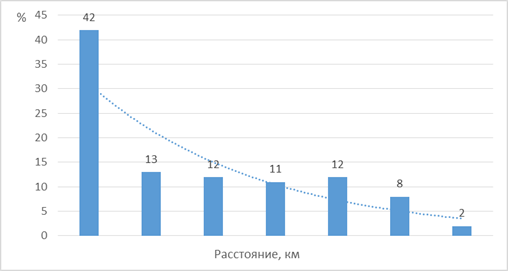
Кроме того, они могут быть двухмодальными, многомодальными. Это говорит о неоднородности выборки, наличии в ней двух или более групп объектов, существенно отличных между собой. Тогда всю совокупность объектов целесообразно разбить на несколько классов по качеству и анализировать их раздельно.

Способы обработки выборки [1]