Основные статистические понятия

Случайная величина. Величина, значение которой при постоянных внешних условиях непредсказуемо, т.е. может меняться от случая к случаю в результате измерений или экспериментов, проводимых при абсолютно одинаковых внешних условиях.

Случайное событие. Всякий эксперимент, всякое измерение, в результате которых находится конкретное значение случайной величины. Случайная величина, случайное событие могут изменяться также под действием неслучайных факторов. Например, цена объекта недвижимости изменяется в зависимости от его размера и удаления от центра города. Однако в ряде случаев закономерность таких изменений неизвестна или конкретная задача не требует их учета. Тогда и эти факторы относят к разряду случайных.

Генеральная совокупность. Совокупность всех возможных реализаций случайной величины. В большинстве практических ситуаций данные генеральной совокупности не доступны, а доступны данные только какой-то ее части – выборки.

Генеральная совокупность может подразделяться на группы (подсовокупности) по определенному признаку (неслучайному фактору). Например, жилой фонд и сделки – по подвидам объектов, районам (зонам) города, классам объектов, размерам помещений и т.д. Доля подсовокупностей каждого типа характеризует структуру генеральной совокупности.

Структура генеральной совокупности – это доля (процентный состав в ней подсовокупностей, выделенных по одному или нескольким признакам.

Примеры описания структуры генеральной совокупности приведены на рисунке 1. [1]

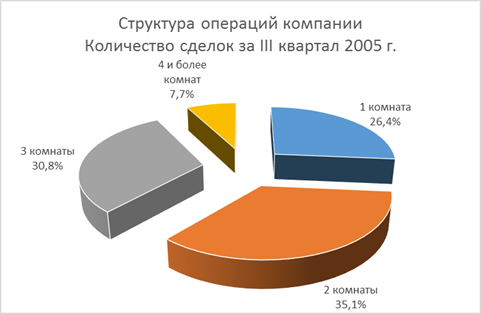
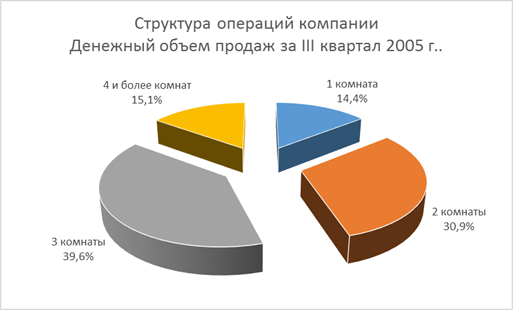
Рисунок 1. Примеры описания структуры генеральной совокупности

Выборка из генеральной совокупности или просто выборка. Множество наблюдений случайной величины, являющееся подмножеством генеральной совокупности. Значения случайной величины, выбранные из генеральной совокупности по случайному признаку.

Например, все сданные в аренду за определенный период объекты в городе являются выборкой из нежилого фонда.

Репрезентативность выборки. Выборка называется репрезентативной (представительной), если она достаточно полно описывает особенности генеральной совокупности. Если о генеральной совокупности ничего не известно, то единственной гарантией репрезентативности выборки может служить случайный отбор.

Дискретная случайная величина. Множество допустимых значений случайной величины дискретно. Дискретная случайная величина способна принимать значения из конечного или счетного множества допустимых значений.

Непрерывная случайная величина – множество допустимых значений случайной величины непрерывно. Непрерывная случайная величина определяется бесконечным множеством допустимых значений из некоторого непрерывного промежутка.

Закон распределения случайной величины. Всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями.

Вероятностный ряд. Пусть дискретная случайная величина X может принимать значения x₁, x₂, ..., x_K с вероятностями p₁, p₂, ..., p_K соответственно. Упорядоченную по возрастанию последовательность значений случайной величины X обозначим как x^MIN=x¹≤x²≤...≤x^K=x^MAX. Тогда последовательность пар (xⁱ,pⁱ) дискретной случайной величины, где pⁱ – вероятность реализации значения xⁱ, называют вероятностным рядом.

Таблица 1.

Вероятностный ряд представляет закон распределения, заданный в табличном виде.

Закон распределения F(x) дискретной случайной величины X, выраженный в аналитической форме:

.

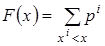Закон распределения дискретной случайной величины F(x) показывает вероятность того, что значение случайной величины X будет меньше x, то есть

F (x)=P(X<x).

Для непрерывной случайной величины X рассматривают вероятность того, что значение случайной величины попадет в некоторый интервал. Для этого используется вероятностью события X<x, где x – произвольное действительной число. Закон (функция) распределения непрерывной случайной величины:

F (x)=P(X<x).

Плотность функции распределения(плотность распределения) непрерывной случайной величины f(x) – производная от функции распределения F(x): f(x)=dF(x)/dx.

Моменты случайной величины.

На практике, если функции распределения F(x) случайной величины X неизвестна, то для описания случайной величины X используют моменты случайной величины, которые являются вещественными числовыми параметрами (характеристиками), выражающими характерные особенности случайной величины. Моменты случайной величины являются интегральными характеристиками распределения. Для дискретной и непрерывной случайной величины начальным моментом k-го порядканазывается величина:

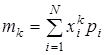и ,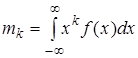

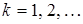
Начальный момент первого порядка m₁ (k=1) называется математическим ожиданием(средним значением) случайной величины X и обозначается M[X], m_x.

, .

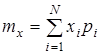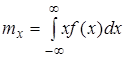Центральным моментом k-го порядкадля дискретной и непрерывной случайной величины называется

, , .

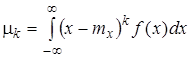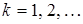Первый центральный момент μ₁ всегда равен 0, μ₁=0. Второй центральный момент μ₂ называется дисперсией. Обозначается: D[X], D_x, σ²_x или σ².

Среднее квадратичное отклонение (стандартное отклонение) σ_x– корень квадратный из дисперсии.

Коэффициент асимметрииγ – третий центральный момент, деленный на σ³_x:

.

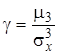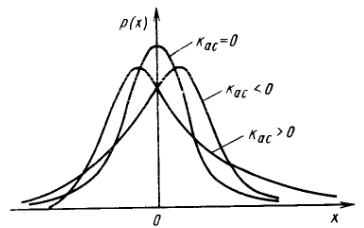
Рисунок 2. Зависимость коэффициента асимметрии от кривых распределения

Коэффициент эксцесса(мера остроты пика функции плотности) δ:

.

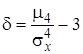(Число 3 вычитается для того, чтобы коэффициент эксцесса нормального распределения был равен нулю, δ=0. Это удобно при сравнении остроты пика различных распределений между собой и с нормальным распределением.)

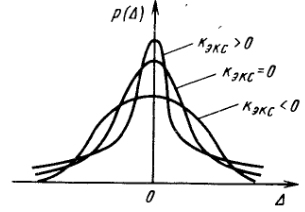
Рисунок 3. Зависимость коэффициента эксцесса от кривых распределения

Медиана m определяет такое значение случайной величины, которое делит распределение на две равновероятные половины. Для дискретного распределения случайной величины номер значения m, являющегося медианой, определяется соотношениями:

.

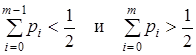Модойμ называется такое значение случайной величины, которое является точкой максимума для плотности распределения. Обычно в статистике имеют дело с унимодальными распределениями, т.е. с распределениями с одной точкой максимума.

В унимодальном распределении математическое ожидание, медиана и мода располагаются либо в перечисленном порядке, либо в обратном. Если распределение симметрично, то m_x=m=μ. Математическое ожидание, медиана и мода являются мерой взаимного расположения значений случайной величины, а дисперсия σ²_x показывает характер разброса значений случайной величины.

Коэффициент вариации –это отношение среднего квадратичного отклонения к среднему. Характеризует относительную величину рассеяния случайной величины и позволяет сравнивать по степени разброса случайные величины с различными средними.

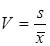
Классическим распределением, для которого наиболее развиты расчетные методы, является гауссовское или нормальное распределение.

Нормальное распределение непрерывной случайной величины X – распределение, для которого плотность распределения вероятности определяется формулой:

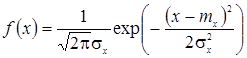
В симметричном распределении, близком к нормальному, в интервале ±σ располагаются 68 % значений случайной величины, в интервале ±2σ – 95%, ±3σ около 97,7%.