Расчет статистических показателей выборки. Средняя арифметическая и средневзвешенная.

1. Объем выборки – равен числу случайных величин, входящих в выборку.

2. Расчет средних величин для различных случаев может проводиться тремя способами. Первый чаще применяется для первичного рынка, когда неизвестны площади квартир либо когда они различаются незначительно (например, для квартир с одинаковым числом комнат) второй – когда площади известны, а главное, когда площади объектов (коттеджей, офисов и т.д.) существенно различаются. При первом способе рассчитывается средняя (среднеарифметическая) удельная цена предложения квартир в выборке, а при втором и третьем – средневзвешенная удельная цена предложения (или цена 1 кв. м.).

Первый способ: средняя удельная цена предложения объектов определяется делением суммы цен квадратного метра объектов на их количество в выборке.

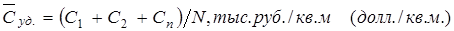
С₁ – цена 1 кв. м. общей площади объекта (удельная цена предложения объекта), N – число объектов в выборке.

Второй способ: средняя цена предложения 1 кв. м в выборке определяется делением суммы полных цен на объекты на сумму площадей объектов («бухгалтерский метод»)

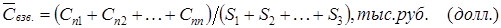
C_ni – полная цена i-го объекта, S_i – общая площадь i-го объекта.

Третий способ средневзвешенная удельная цена предложения (средняя цена 1 кв. м) и средневзвешенная арендная ставка определяются по формуле средневзвешенного арифметического, с учетом площадей объектов:

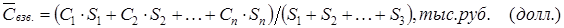
C₁, A₁ – удельная цена, арендная ставка первого объекта,

N – число объектов в выборке.

Результат вычисления по формулам ко второму и третьему способам совпадает, поэтому среднюю цену 1 кв. м можно называть средневзвешенной по площади помещений удельной ценой в выборке и измерять в тыс. руб./кв. м. (долл./кв. м.)

3. Размах варьирования представлен наименьшим и наибольшим значением выборки C_min, C_max.

4. Оценка дисперсии и среднеквадратического отклонения.

5. Исключение выскакивающих значений. После определения дисперсии необходимо исключить из выборки крайние (справа и слева) «выскакивающие» значения и заново рассчитать параметры выборки. При этом для симметричных распределений, близких к нормальному применяется правило «трех сигм» Исключаются значения, лежащие за пределами доверительного интервала в плюс/минус три среднеквадратических отклонения. Это соответствует доверительной вероятности 0.977 (т.е. исключаются из рассмотрения примерно 2 % крайних значений). Применяются и более жесткие критерии, например, две сигмы (доверительная вероятность 0.95).

Для асимметричных распределений, какими являются распределения цен, арендных ставок на рынке недвижимости (обычно слева «поджато», справа растянуто) авторы [1] рекомендуют модифицированное правило трех сигм» значение C_i отбрасывается, если

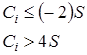
Дополнительная проверка на количество исключаемых точек, которое не должно превышать 1 % слева и справа. В противном случае соответствующий критерий сдвигается влево (или, соответственно, вправо) на 0,5S.

Важно отметить, что исключение выскакивающих значений проводится в малых выборках, т. е после максимального расчленения общей выборки по местоположению, качеству, размеру и другим признакам. Затем статистические параметры объединенных и расчлененных выборок пересчитываются (один раз).

6. Оценка погрешности в определении среднего

Приближенная оценка погрешности в определении средневыборочного при доверительной вероятности 0.95 равна

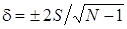
Наличие данных о погрешности в определении средних цен позволяет при сравнении двух выборок, например, по двум различным районам, или типам объектов, или за два различных месяца) использовать следующее правило: выборки считаются различающимися незначительно, если разность их средних меньше суммы половины погрешностей.

Литература

1. Стерник Г. М. Анализ рынка недвижимости для профессионалов /Г. М. Стерник, С. Г. Стерник. – Москва: Экономика, 2009. – 605, [1] с.: ил., цв. ил.; 27 см. – Библиогр. в конце кн.