ПРИЛОЖЕНИЕ Е. β-спектры

Для очень большого числа N β-распадов число распадов dN, при которых произойдет вылет электрона с импульсом от p_e до p_e + dp_e и антинейтрино с импульсом p_ν, определяется как

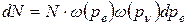, (Е.1)

где ω(p_e) и ω(p_ν) – вероятности того, что проекции импульсов p_e и p_ν примут значения p_e и p_ν соответственно. Для каждой из двух частиц вероятность ω(p) пропорциональна площади сферы с радиусом р, т.е.

.

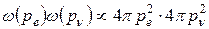Перейдем от импульсов частиц к их энергиям. Кинетическая энергия электрона как релятивистской частицы

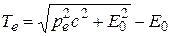
(E₀ = m_ec²), откуда следует

.

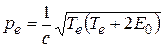Дифференцируя T_e по p_e, получим

,

.

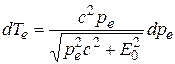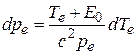Вследствие малой массы нейтрино с любой энергией можно считать ультрарелятивистским, поэтому p_ν = E _ν/c. Учтем закон сохранения энергии,[208] согласно которому 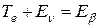. Тогда

.

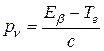В результате подстановки p_e, p_ν и dp_e в (Е.1) найдем, что число распадов, при которых произойдет вылет электрона с энергией от T_e до T_e + dT_e

,

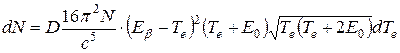где D – коэффициент пропорциональности. Таким образом, выражающая форму β-спектра функция 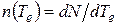имеет вид

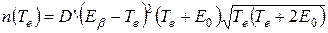. (8.1)

При малых энергиях β-частиц форма спектра заметно искажается из-за кулоновского взаимодействия β-частиц с ядром, которое «включается» сразу же после распада. В случае β^–-распада это взаимодействие является притягивающим и стремится уменьшить энергию вылетающего электрона. При β⁺-распаде кулоновское взаимодействие – отталкивающее и поэтому стремится ускорить вылетающий позитрон. В результате спектры электронов обогащаются, а спектры позитронов обедняются частицами с низкой энергией (рис. Е). Учет кулоновского взаимодействия приводит к следующей формуле для распределения β-частиц по энергиям:

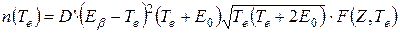, (E.2)

где функция 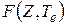точно вычисляется и протабулирована для различных значений заряда ядра и энергии β-частиц. В нерелятивистском приближении

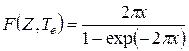, (E.3)

где x = ±Ze²/ћv (v – скорость β-частицы, Z – заряд дочернего ядра, знак «+» соответствует электронам, «–» позитронам).