ПРИЛОЖЕНИЕ Г. Биномиальное распределение, распределения Пуассона и Гаусса

Обозначим биномиальное распределение (5.8) как 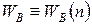и вычислим для него среднее число ядер 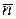, распадающихся за некоторый промежуток времени. Для этого введем функцию

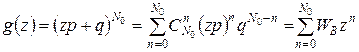
и найдем ее первую и вторую производные по параметру z в точке z = 1:

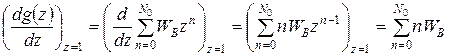, (Г.1)

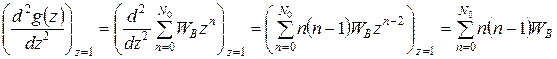. (Г.2)

Согласно определению среднего,

.

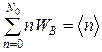Тогда, в силу (Г.1)

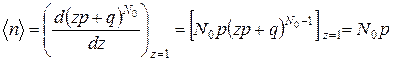. (5.10)

Чтобы найти дисперсию биномиального распределения, разложим выражение для квадрата отклонения случайной величины от среднего:

.

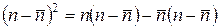Можно видеть, что при усреднении второго слагаемого в этом выражении получается нуль, так как среднее отклонение от среднего равно нулю. Далее представим первое слагаемое в следующем виде:

.

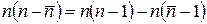Используя определение дисперсии, найдем, что

.

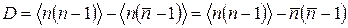Далее воспользуемся тем, что, согласно (Г.2), среднее значение произведения n(n – 1) есть вторая производная функции g(z). Отсюда

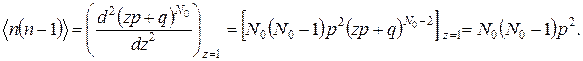
Тогда

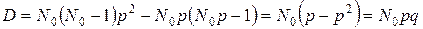. (5.11)

При 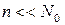и р << 1 выражение (5.8) можно упростить. Подставляя, согласно (5.10), 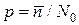получаем:

.

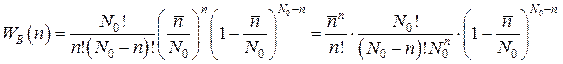Осуществим предельный переход 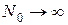во втором множителе:

.

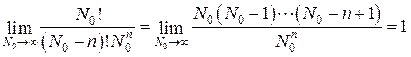Аналогично, пользуясь определением второго замечательного предела

,

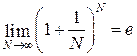получаем для третьего множителя

.

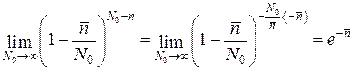Таким образом,

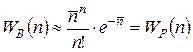. (5.12)

Полученное распределение W_P(n) известно как распределение Пуассона.

Преобразуем соответствующим образом распределение Пуассона для 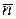>>1. Во-первых, воспользуемся формулой Стирлинга для аппроксимации факториалов больших чисел .

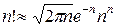Тогда

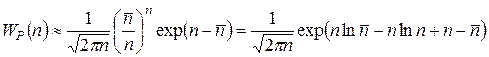. (Г.3)

Во-вторых, используем тот факт, что распределение W_Р(n) заметно отлично от нуля лишь в довольно узкой области справа и слева от максимума (см. рис. 5.2). Тогда, раскладывая показатель экспоненты в (Г.3) в ряд Тейлора по ,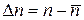

,

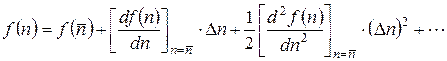с точностью до первого неисчезающего члена (в данном случае – второго порядка по Δn) и заменяя под корнем 2πn на 2π 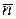, получаем

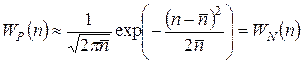. (5.14)

Выражение (5.14) представляет собой не что иное, как закон Гаусса, или нормальное распределение непрерывной случайной величины.[207]