Основи рентгенографії

Діапазон довжин хвиль рентгенівських променів ∆l=10^-8 – 10^{-14 м (10 - 10-5} нм) дозволяє отримувати дифракційні картини від кристалічних зразків. До цього діапазон своїми довжинами хвиль потрапляє як гальмівне (суцільний спектр), так і характеристичне (лінійчастий спектр). У зв’язку з цією особливістю рентгенівських променів історично було започатковано два методи досліджень, які не втратили своєї актуальності. Перший із них – це метод Лауе, суть якого полягає в у спектроскопії гальмівного рентгенівського випромінювання, тобто у встановленні діапазону довжини хвиль. Для цього гальмівне випромінювання направляється на монокристал певної речовини з відомими d_hkl. Велика кількість кристалографічних площин завжди відповідає умові рівняння Бреггів (співвідношення (6.1)), що дасть можливість визначити експериментально кути дифракції і величину l.

Другий із них метод Дебая-Шерера, який покладено в основу рентгено-фазового аналізу полікристалів, багато в чому подібний до розглянутого вище електронографічного методу. Оскільки полікристалічний зразок містить велику кількість кристалітів, то завжди частина із них буде зорієнтована таким чином, що сформується система дифракційних максимумів з різними кутами дифракції. Приклади дифракційних картин (рентгенограм) представлені на рис. 6.20.

В основу РГ покладено фактично ті самі рівняння, що й у випадку ЕГ, але суттєва відмінність полягає у відсутності поняття стала приладу (формула (6.2)), оскільки рентгенівські кути дифракції можуть становити величину порядку 10 і 100 градусів, що забезпечує високу точність розрахунків sin Θ. У такому разі, скориставшись рівнянням Бреггів, ми можемо записати

,

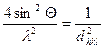а рівняння (6.4) подати у вигляді

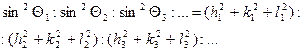(6.7)

Це друге рівняння рентгенографії, яке відіграє таку саму роль, як і (6.4) в електронографії.

Оскільки відношення суми квадратів індексів Міллера утворює ряд дробових (таблиця 6.5) або цілих чисел (співвідношення (6.5)), то це дозволяє установити тип кристалічної решітки і розрахувати за формулами (6.6) або подібними до них параметри кристалічної гратки. Формулу (6.6) ми трактуємо як третє рівняння РГ. При розшифруванні рентгенограм від складних сингоній необхідно користуватися теоретичними номограмами Бьордстрема.

Можливості РГ не вичерпуються лише проведенням рентгенофазового аналізу. Оскільки кутова ширина дифракційної лінії ∆Θ обернено пропорційна середньому розміру кристалітів, то це дає можливість вивчати ступінь дисперсності зразків. За величиною ∆Θ та асиметрією дифракційних максимумів можна також розрахувати тип і концентрацію дефектів пакування, рівень мікронапружень кристалічної гратки, характер і ступінь орієнтації текстури тощо.

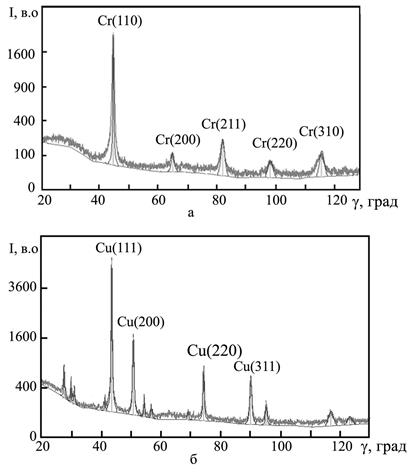
Рисунок 6.20 – Приклад рентгенограм від полікристалічних зразків ОЦК-Cr (а) і ГЦК-Cu (б)

Закінчуючи цей підрозділ, вкажемо також на такий прикладний аспект РГ, як використання її в медицині. У цьому відношенні надзвичайно великий внесок зроблений видатним вченим Австро-Угорської імперії, вихідцем із України І.П. Пулюєм (1845-1918), який отримав ступінь доктора наук у Страсбурзькому університеті й у
1880-90-х рр. працював завідувачем кафедри фізики, ректором Німецької Політехніки у Празі. У 1896 р. він опублікував декілька робіт про дослідження властивостей рентгенівських променів (на цьому етапі він до деякої міри випереджав доцента Берлінського університету К. Рентгена, з іменем якого пов’язують відкриття і пояснення природи рентгенівських променів). І. Пулюй у цей період організував виготовлення рентгенівських трубок (тоді вони називалися трубки Пулюя), які знайшли своє застосування в медицині (як свідчать документи І. Пулюю вдалося отримати найбільш якісні на той час рентгенівські знімки людських органів).

Широке застосування рентгенівські промені також знайшли у такому неруйнівному методі контролю якості металевих виробів, як дефектоскопія.