Основи електронографії
В основу електронографії покладено чотири основні формули. Перша із них - рівняння Бреггів у вигляді формули (6.1). Друге співвідношення пов’язує між собою діаметри кілець (Dhkl) і міжплощинні відстані (dhkl) за допомогою т.зв. сталої приладу C = 2λL. Для отримання цього співвідношення скористаємося геометрією рис 6.14, із якої випливає, що
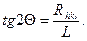
Оскільки кути Θ в електронографії мають малі величини (до 4º), то
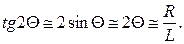
Поряд з цим рівняння (6.1) можна спростити до вигляду:
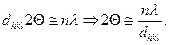
Маючи два співвідношення для 2Θ, можна записати для випадку n = 1
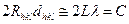
або через діаметр даного кільця:
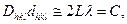 (6.2)
(6.2)
де С - стала приладу, яка не залежить від номера дифракційного кільця.
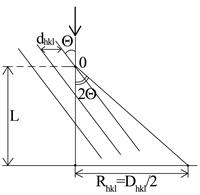
| Рисунок 6.14 – До отримання співвідношення для сталої приладу |
Оскільки L за своєю суттю є фокусною відстанню лінзи, яка може змінювати свою величину залежно від умов фокусування, то формула (6.2) дає неточне значення сталої С. Тому більш коректно і правильно буде розрахувати С, використовуючи т.зв. еталон. Залежно від необхідної точності знаходження dhkl як еталон можна використовувати рекристалізовану плівку Al (товщина – 30 – 40 нм), що забезпечить Δdhkl близько ±0,002 нм (якщо цей еталон буде нанесений на зразок, то можна досягти Δdhkl = ±0,001 нм). Більш високоточним є еталон із плівок MgO, NaCl, TlCl. Для всіх еталонів загальною вимогою є точна інформація про dhkl і їх слабка залежність від товщини зразка і розміру кристалітів. При нанесенні цих еталонів на зразок (одночасна зйомка електронограми) можна досягти максимальної точності Δdhkl = ±0,0005 нм (це т.зв. прецизійне вимірювання dhkl).
Оскільки формула (6.2) має загальний характер безвідносно до зразка, то її можна переписати таким чином:
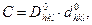 (6.2′)
(6.2′)
де індекс ”нуль” означає еталон.
Таблиця 6.4 ілюструє методику розрахунку С.
Зауважимо, що вимірювання діаметрів 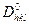 необхідно здійснювати з якомога високою точністю (наприклад, ±0,1 мм). Для цього використовуються спеціальні прилади – компаратори, мікрофотометри та ін.
необхідно здійснювати з якомога високою точністю (наприклад, ±0,1 мм). Для цього використовуються спеціальні прилади – компаратори, мікрофотометри та ін.
Таблиця 6.4 – Визначення сталої приладу за допомогою еталона із плівки Al
| №/№ | 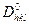 , м , м
| hkl | 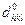
| 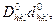 м∙нм м∙нм 
|
| ∙∙∙ | 0,2338 | ∙∙∙ | ||
| ∙∙∙ | 0,2025 | ∙∙∙ | ||
| ∙∙∙ | 0,1432 | ∙∙∙ | ||
| ∙∙∙ | 0,1221 | ∙∙∙ | ||
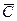 =∙∙∙ =∙∙∙
|
Таким чином, знайшовши сталу приладу, ми пройшли перший етап фазового аналізу. Другим етапом буде розрахунок dhkl невідомого зразка на основі вимірювання Dhkl за допомогою отриманої електронограми і формули
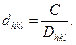 (6.2′′)
(6.2′′)
Третій етап найбільш складний, оскільки на ньому вирішується основне завдання фазового аналізу - встановлення типу кристалічної ґратки та індексів Міллера (hkl) для усіх ліній. Для цього необхідно скористатися формулами для т.зв. квадратичних форм (одна із цих форм буде третьою формулою електронографії). Для кожної із семи кристалографічних сингоній квадратичні форми зовні відрізняються, хоча фізична суть у них однакова – це зв'язок між величинами dhkl, параметрами аhkl і сhkl та індексами Міллера. Для найбільш простих сингоній квадратичні формули мають такий вигляд:
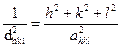 (кубічна сингонія),
(кубічна сингонія),
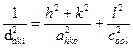 (тетрагональна сингонія), (6.3)
(тетрагональна сингонія), (6.3)
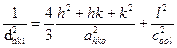 (гексагональна сингонія),
(гексагональна сингонія),
де параметри ґратки в межах даної сингонії - сталі величини.
Подальший аналіз буде проведений на прикладі кубічної сингонії, яка поєднує в собі три типи кристалічних ґраток (ґратки Браве): просту кубічну (ПК), об’ємноцентровану кубічну (ОЦК) та гранецентровану кубічну (ГЦК) (рис. 6.15).
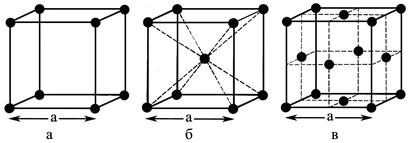
Рисунок 6.15 – Типи кристалічних ґраток кубічної сингонії: а – ПК, б – ОЦК, в – ГЦК
Скориставшись квадратичною формою, можна отримати очевидне співвідношення
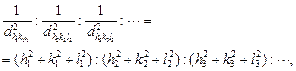 (6.4)
(6.4)
яке являє собою третю формулу електронографії.
Оскільки у правій частині маємо відношення суми квадратів індексів Міллера, то це для кожного типу ґраток будуть певні числа. Щоб їх розрахувати, необхідно скористатися деякими даними кристалографії. Зокрема, із теорії кристалів відомо, що ПК дає дифракційні відбиття із усіма можливими індексами, тобто: (100), (110), (111), (200), (210), (211), (220) і т.д. У випадку ОЦК ґратки структурно забороненими відбиттями (тобто, вони не спостерігаються на електронограмі) є ті, в яких сума (h+k+l) – число непарне, а у випадку ГЦК ґратки не спостерігаються лінії, для яких h, k і l – числа різної парності (прийнято вважати, що 0 – парне число). Ці дані дозволяють розрахувати відношення 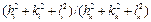 й установити тип решітки (таблиця 6.5).
й установити тип решітки (таблиця 6.5).
Хоча інколи ряд чисел у вигляді відношення суми квадратів індексів зручніше подати у вигляді 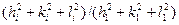 . Тоді для кожного типу кубічної гратки він простіший, а саме:
. Тоді для кожного типу кубічної гратки він простіший, а саме:
ПК, ОЦК: 1, 2, 3, 4, 5, 6, 8, 9, … (6.5)
ГЦК: 1, 1,33; 2,66; 3,67; 4; 5,33; …
Отримавши міжплощинні відстані і взявши відношення їх квадратів у вигляді
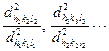 відповідно до формули (6.4),
відповідно до формули (6.4),
або у більш зручній формі
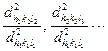 відповідно до останнього зауваження, ми можемо установити відповідність типу ґратки ГЦК чи ОЦК або ПК. Для того, щоб розрізнити два останні типи ґраток, необхідно провести додатковий аналіз, суть якого полягає в аналізі інтенсивностей ліній та їх взаємного положення на електронограмах. Крім цього, необхідно завжди мати на увазі той факт, що в однокомпонентних металевих речовинах ПК ґратки не спостерігаються.
відповідно до останнього зауваження, ми можемо установити відповідність типу ґратки ГЦК чи ОЦК або ПК. Для того, щоб розрізнити два останні типи ґраток, необхідно провести додатковий аналіз, суть якого полягає в аналізі інтенсивностей ліній та їх взаємного положення на електронограмах. Крім цього, необхідно завжди мати на увазі той факт, що в однокомпонентних металевих речовинах ПК ґратки не спостерігаються.
Стосовно інтенсивностей, то експериментальні й розрахункові дані говорять про те, що найбільш інтенсивною лінією може бути довільна лінія (рис. 6.16 ілюструє розподіл інтенсивностей ліній на електронограмах від ПК, ОЦК і ГЦК ґраток). Зауважимо, що при розрахунках електронограм треба мати на увазі, що три типи кристалічних ґраток (ПК, ОЦК і ГЦК) об’єднують 24 структурні види кубічних решіток, наприклад: ОЦК типу α-Fe, CsCl, Mn2O3; ГЦК типу Al,
Таблиця 6.5 – Відношення суми квадратів індексів Міллера для ПК, ОЦК і ГЦК ґраток
| № | ПК | ОЦК | ГЦК | ||||||
| hkl | 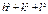
| 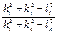
| hkl | 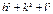
| 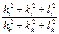
| hkl | 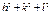
| 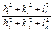
| |
| 0,50 | 0,50 | 0,75 | |||||||
| 0,68 | 0,68 | 0,50 | |||||||
| 0,75 | 0,75 | 0,72 | |||||||
| 0,80 | 0,80 | 0,91 | |||||||
| 0,83 | 0,83 | 0,75 | |||||||
| 0,75 | 0,85 | 0,78 | |||||||
| 0,89 | 0,87 | 0,80 | |||||||
| або | – | – | – |
NaCl, CaF2, Cu2O і т.д.; ПК типу W3O, Cr2O3, шпінелі (γ- Fe2O3) і т.д. Для кожного структурного виду має місце свій розподіл інтенсивностей. Так, у ГЦК ґратках типу Al найбільша інтенсивна лінія (111); типу NaCl – (110) і т.д.
Стосовно взаємного розміщення ліній на електронограмах, то воно має притаманний кожному типу ґраток характер (рис. 6.17 ілюструє це на прикладі ПК, ОЦК і ГЦК ґраток). Зокрема, у випадку ПК ґратки лінії монотонно зближуються (за геометричною прогресією) при збільшенні кута відбиття; для ОЦК ґратки характерним є розрив між лініями (110) і (200) з подальшим зближенням інших ліній; розподіл ліній ГЦК структури також має свою особливість – спочатку дві лінії, знову дві з лінією (222) поряд, потім далі попарно із постійним зменшенням відстані між парними лініями. Зазначені особливості розподілу ліній та їх інтенсивностей необхідно враховувати для коректного розшифрування

Рисунок 6.16 – Електронограми від різних ґраток кубічної сингонії: а, б – ПК (Cr2O3 і CrO3); в – ОЦК (Cr); г – ГЦК (Ni)
електронограми.
У випадку тетрагональної і гексагональної сингоній, які також мають багато структурних типів, відносно просто розшифрувати електронограму за допомогою ліній, в яких нульові або третій, або два перші індекси Міллера (див. формулу (6.3)). Оскільки кінцевою метою фазового аналізу є не тільки установлення типу кристалічної ґратки,
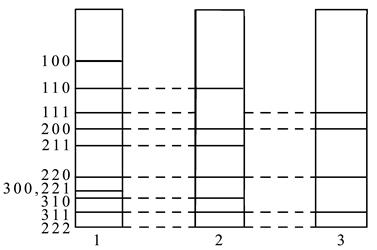
Рисунок 6.17 – Схема електронограм від ПК (а), ОЦК (б) і ГЦК (в) ґраток
а й розрахунок їх параметрів, то четвертою формулою слід вважати варіанти (6.3), а саме:
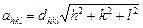 - кубічна сингонія;
- кубічна сингонія;
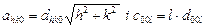 - тетрагональна сингонія; (6.6)
- тетрагональна сингонія; (6.6)
|
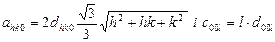 - гексагональна
- гексагональна
Однак для фазового аналізу інших шести сингоній в самому загальному випадку необхідно користуватися т.зв. номограмами Бьордстема, усі можливі варіанти яких наведені у літературних джерелах до шостого розділу.
Дата добавления: 2015-05-26; просмотров: 1662;
