Теоретичні відомості і методичні вказівки. Логічні функції, приведені в табл
Бульова алгебра
Логічні функції, приведені в табл. 3.1, можна розглядати як елементарні операції над однією чи двома двійковими змінними. Функціонально повна система таких операцій утворить на безлічі двозначних змінних алгебру логіки. Таких алгебр можна представити стільки ж, скільки набереться придатних функціонально повних систем. Але найбільш поширена бульова алгебра, у якій як основні операції прийняті кон‘юнкция 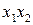 (І), дизюнкція
(І), дизюнкція 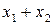 (АБО) і заперечення
(АБО) і заперечення 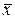 (НІ). Часто кон‘юнкцію і диз‘юнкцію називають відповідно логічним добутком і сумою, а заперечення - інверсією. Використовуються також інші варіанти позначень: для конюнкции
(НІ). Часто кон‘юнкцію і диз‘юнкцію називають відповідно логічним добутком і сумою, а заперечення - інверсією. Використовуються також інші варіанти позначень: для конюнкции 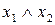 , для диз'юнкції
, для диз'юнкції 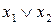 і для заперечення
і для заперечення 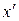 . Щоб уникнути в складних формулах зайвих дужок, що з'являються при суперпозиції функцій, установлений твердий порядок виконання операцій - конюнкция передує диз'юнкції. Властивості бульових операцій І, АБО, НІ визначаються таблицями відповідних функцій (див. табл. 3.1) і можуть бути представлені у виді
. Щоб уникнути в складних формулах зайвих дужок, що з'являються при суперпозиції функцій, установлений твердий порядок виконання операцій - конюнкция передує диз'юнкції. Властивості бульових операцій І, АБО, НІ визначаються таблицями відповідних функцій (див. табл. 3.1) і можуть бути представлені у виді
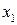 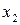
| 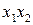
| 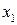 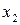
| 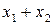
| 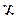
| 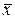
| ||
| 0 0 0 1 1 0 1 1 | 0 0 0 1 1 0 1 1 | ||||||
Тут використана інша форма таблиці відповідності, у якій усілякі комбінації значень змінних записуються по рядках, а для значень функції при цих комбінаціях приділяється стовпець. Використання тієї чи іншої форми в конкретних випадках обумовлено зручністю, а часто і просто звичкою.
З приведених визначень бульових операцій випливають основні властивості бульової алгебри (табл. 3.3), які можна доводити методом повної індукції, тобто перевіркою для всіх можливих комбінацій значень змінних. Будь-які властивості бульової алгебри можна також довести аналітично без звертання до таблиць відповідності на основі перших п'яти властивостей, що грають при цьому роль аксіом. Наприклад, ідемпотентність, дизюнкцій доводиться наступними перетвореннями: 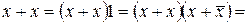
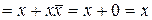 . Варто підкреслити, що знак рівності у формулах алгебри логіки не має кількісного змісту і означає рівносильність функцій у лівій і правій частинах. Дві функції вважаються рівносильними, якщо при будь-яких значеннях аргументів вони приймають однакові значення.
. Варто підкреслити, що знак рівності у формулах алгебри логіки не має кількісного змісту і означає рівносильність функцій у лівій і правій частинах. Дві функції вважаються рівносильними, якщо при будь-яких значеннях аргументів вони приймають однакові значення.
Властивості бульової алгебри використовуються для перетворення і спрощення логічних формул, а також для доведення теоретичних положень. Комутативність і асоціативність дозволяють виконувати операції І и АБО, групуючи змінні в будь-якому порядку. Перша форма дистрибутивності вказує на допустимість винесення загального множника за дужки, як у звичайній алгебрі. Але друга форма в звичайній алгебрі аналога не має, що є одним з основних відмінностей її від алгебри логіки. Властивості заперечення підкреслюють природу взаємного доповнення логічних змінних. Повтори змінної і константи дозволяють рятуватися від постійних доданків і множників або при необхідності вводити їх. Подвійне заперечення не змінює змінну, що можна розглядати як порожню операцію. На основі ідемпотентності можна видаляти повторювані змінні, внаслідок чого в бульовій алгебрі не мають сенсу показники ступеня і числових коефіцієнтів, що також істотно відрізняє її від звичайної алгебри. Закони де Моргана дозволяють звести заперечення складного виразу до заперечення окремих змінних. Останні чотири властивості (склеювання, поглинання, заміщення і виявлення) корисні при різних перетвореннях і спрощеннях бульових формул.
Таблиця 3.3
| Властивості | Перша форма (') | Друга форма (") |
| 1. Комутативність | 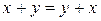
| 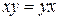
|
| 2. Асоциативність | 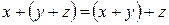
| 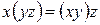
|
| 3. Дистрибутивність | 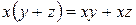
| 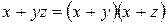
|
| 4. Доповнення | 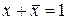
| 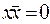
|
| 5. Повтор змінної | 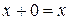
| 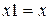
|
| 6. Повтор константи | 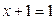
| 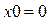
|
| 7. Подвійне заперечення | 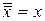
| 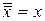
|
| 8. Ідемпотентність | 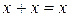
| 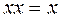
|
| 9. Закони де Моргана | 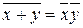
| 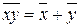
|
| 10. Склеювання | 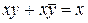
| 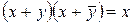
|
| 11. Поглинання | 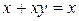
| 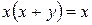
|
| 12. Заміщення | 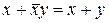
| 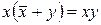
|
| 13. Виявлення | 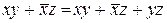
| 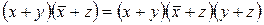
|
Наведені в табл. 3.3 пари властивостей характеризуються специфічною симетрією, яка виражає принцип дуальності алгебри логіки. В кожній парі одні формаотримується з іншої заміною операцій І і АБО , а також констант 0 і 1. В зав‘язку з цим операції І і АБО, як і константи 0 і 1, називаються дуальними. Загалом заміна в будь-якій формулі алгебри логіки кожної операції і константи на дуальні приводить до дуальної формули.
Стандартні форми
Два способи представлення бульової функції - за допомогою логічної формули і таблиці відповідності - взаємно зв'язані між собою в тім, що мається можливість переходити від одного способу до іншого. Побудова таблиці відповідності по логічній формулі розглянуто раніше. Зворотна задача - запис логічної формули по даній таблиці відповідності зважується на основі стандартних форм.
У доконаній диз'юнктивній нормальній формі, називаною також канонічною сумою мінтермів чи стандартною сумою добутків, кожному набору значень змінних, при якому функція дорівнює одиниці, відповідає свій мінтерм. Він виражається як логічний добуток усіх змінних, причому ті змінні, котрі в даному наборі мають значення нуль, входять у добуток із запереченням, а ті що мають значення одиниця - без заперечення. Диз’юнкція (сума) мінтермів, побудованих для всіх наборів з одиничними значеннями функції, і є канонічною сумою мінтермів, що відповідає заданій таблиці істинності.
Інша стандартна форма, дуальна розглянутий вище, називається доконаною кон‘юнктивною нормальною формою. У технічній літературі її також називають канонічним добутком макстермів чи стандартним добутком сум. У цій формі макстерми відповідають тим наборам значень змінних, для яких функція дорівнює нулю. Кожен макстерм являє собою логічну суму всіх змінних, причому ті змінні, котрі для даного наборі мають значення одиниці, входять у суму з запереченням, а ті що мають значення нуль - без заперечення. Кон‘юнкція (добуток) макстермів, побудованих для всіх наборів з нульовими значеннями функції, і є відповідним канонічним добутком макстермів.
Наступний приклад ілюструє запис стандартних форм по заданій таблиці відповідності
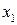
| 0 0 0 0 1 1 1 1 |
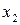
| 0 0 1 1 0 0 1 1 |
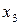
| 0 1 0 1 0 1 0 1 |
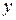
| 0 1 1 0 1 1 0 1 |
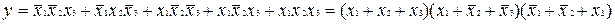 .
.
Якщо бульова функція задана логічною формулою, то її можна привести до стандартної форми послідовністю еквівалентних перетворень, заснованих на властивостях бульової алгебри. Спочатку за допомогою теорем де Моргана вихідний вираз приводиться до такого виду, щоб знаки заперечення відносилися тільки до окремих змінних. Потім на основі властивостей дистрибутивності здійснюється перетворення до однієї з форм – сум добутків чи добутків сум. На заключному етапі використовуються властивості 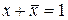 і
і 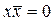 для введення відсутніх змінних у мінтерми і макстерми, а також властивості ідемпотентності
для введення відсутніх змінних у мінтерми і макстерми, а також властивості ідемпотентності 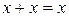 і
і 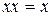 для виключення повторюваних доданків і співмножників. Наприклад, функція
для виключення повторюваних доданків і співмножників. Наприклад, функція 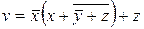 попередньо перетвориться до виду
попередньо перетвориться до виду 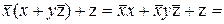
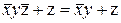 після чого маємо:
після чого маємо:
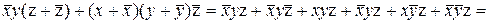
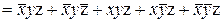
(канонічна сума мінтермів) чи
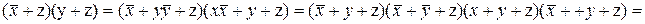
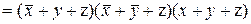
(канонічний добуток макстермів). Відповідна таблиця істинності має вид
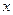
| 0 0 0 0 1 1 1 1 |
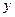
| 0 0 1 1 0 0 1 1 |
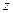
| 0 1 0 1 0 1 0 1 |
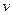
| 0 1 1 1 0 1 0 1 |
Як стандартні розглядаються також нормальні форми, мінтерми (чи макстерми) яким на відміну від доконаних нормальних (канонічних) форм не обов'язково повинні містити всі змінні даної функції. У залежності від числа 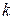 змінних які у них входять, вони називаються мінтермами (чи макстермами)
змінних які у них входять, вони називаються мінтермами (чи макстермами) 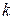 -гo рангу. Дана функція представляється єдиною канонічною формою, але відповідних їй еквівалентних нормальних форм може бути різна кількість. Пошук серед них мінімальних форм є однієї з головних задач синтезу логічних схем.
-гo рангу. Дана функція представляється єдиною канонічною формою, але відповідних їй еквівалентних нормальних форм може бути різна кількість. Пошук серед них мінімальних форм є однієї з головних задач синтезу логічних схем.
Перетворення і спрощення формул
Основні властивості бульової алгебри дозволяють здійснювати еквівалентні перетворення формул для їхнього чи спрощення приведення до необхідного виду, а також для доказу логічних правил і теорем. Ілюстрацією перетворення бульових виразів може служити, наприклад, доказ властивості виявлення (див. табл. 3.3):
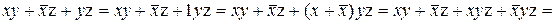
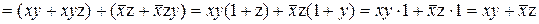 .
.
Тут використані послідовно властивості 5 і 1 , 4', 3', 2' і 1", 3', 1' і 6', 5" (штрихами відзначені відповідно перша і друга форми). Як видно, у виразі 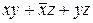 додатковий член
додатковий член 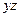 являє собою добуток змінних (чи формул) при
являє собою добуток змінних (чи формул) при 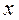 і
і 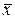 у членах, що
у членах, що 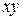 породжують,
породжують, 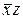 і не впливає на значення цього виразу за умови, що члени, що породжують, присутні.
і не впливає на значення цього виразу за умови, що члени, що породжують, присутні.
Процес спрощення зводиться до послідовного застосування тих чи інших загальних властивостей для того, щоб зменшити загальну кількість змінних які входять у формулу і символів логічних операцій. Тим часом далеко не очевидно, яке з властивостей найбільше доцільно використовувати на кожнім кроці, тому робота з формулами на інтуїтивному рівні подібна блуканню в лабіринті. Цьому процесу можна додати цілеспрямований характер, якщо скористатися властивостями склеювання, поглинання і виявлення, представивши попередньо вихідне виразу в нормальній формі. Надалі перетворення виконуються в диз'юнктивній нормальній формі (сумі мінтермів), а відповідні правила для кон‘юнктивной нормальної, форми (добутку макстермів) можна одержати на основі принципу дуальності.
Склеювання 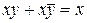 (під
(під 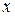 можна розуміти будь-який вираз) дозволяє замінити два мінтерма, що відрізняються входженням тільки однієї змінною (із запереченням і без нього), одним мінтермом більш низького рангу. Нехай, наприклад, функція задана у виді канонічної суми мінтермів:
можна розуміти будь-який вираз) дозволяє замінити два мінтерма, що відрізняються входженням тільки однієї змінною (із запереченням і без нього), одним мінтермом більш низького рангу. Нехай, наприклад, функція задана у виді канонічної суми мінтермів: 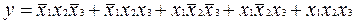 . Групуючи члени і застосовуючи операцію склеювання, маємо
. Групуючи члени і застосовуючи операцію склеювання, маємо
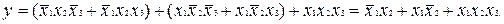
При іншому варіанті групування одержимо
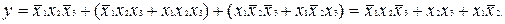
Наступні спрощення засновані на властивостях поглинання, і виявлення. Поглинання 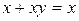 , якщо під
, якщо під 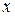 і
і 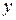 розуміти не тільки змінні, але і будь-які булевы виразу, дозволяє виключити всі мінтерми, у які як співмножник входить деякий інший мінтерм більш низького рангу. Поряд з цим додатковий член, що вводиться на основі властивості виявлення, можна використовувати для поглинання і/або заміщення інших членів (мінтермів). Ця операція, названа узагальненим склеюванням, завжди можлива, якщо вихідна формула поряд із членами, що породжують, містить мінтерми, у які як співмножник входить додатковий член, наприклад:
розуміти не тільки змінні, але і будь-які булевы виразу, дозволяє виключити всі мінтерми, у які як співмножник входить деякий інший мінтерм більш низького рангу. Поряд з цим додатковий член, що вводиться на основі властивості виявлення, можна використовувати для поглинання і/або заміщення інших членів (мінтермів). Ця операція, названа узагальненим склеюванням, завжди можлива, якщо вихідна формула поряд із членами, що породжують, містить мінтерми, у які як співмножник входить додатковий член, наприклад:

 Тут додатковий член поглинув
Тут додатковий член поглинув 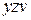 , після чого віддаляється як той що не впливає на значення отриманого виразу. У випадках, коли додатковий член поглинає один із членів, що породжують, його видаляти не можна і, отже, відбувається заміщення цього члена, що породжує. Наприклад:
, після чого віддаляється як той що не впливає на значення отриманого виразу. У випадках, коли додатковий член поглинає один із членів, що породжують, його видаляти не можна і, отже, відбувається заміщення цього члена, що породжує. Наприклад:
Тут додатковий член поглинає мінтерм 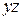 і заміщає мінтерм що його породив
і заміщає мінтерм що його породив 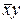 . Зауважимо, що цей вираз можна було б спростити і без введення додаткового члена за допомогою поглинання і заміщення:
. Зауважимо, що цей вираз можна було б спростити і без введення додаткового члена за допомогою поглинання і заміщення: 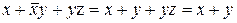 .
.
Застосовуючи викладену процедуру до розглянутого прикладу для першого варіанта групування 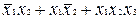 ,
, 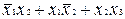 чи одержуємо
чи одержуємо 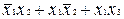 . Аналогічно другий варіант
. Аналогічно другий варіант 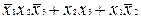 спрощується до виду
спрощується до виду 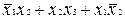 , що повторює вже отриманий результат для першого варіанта. Таким чином, вихідна формула перетвориться до двох форм, що у даному випадку є і мінімальними. До такого ж результату можна було б прийти, застосовуючи тільки простої склеювання, якщо у вихідному вираженні повторити мінтерм
, що повторює вже отриманий результат для першого варіанта. Таким чином, вихідна формула перетвориться до двох форм, що у даному випадку є і мінімальними. До такого ж результату можна було б прийти, застосовуючи тільки простої склеювання, якщо у вихідному вираженні повторити мінтерм 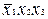 чи
чи 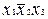 про що, звичайно, не так просто догадатися на самому початку перетворення. Варто помітити, що з застосуванням узагальненого склеювання можна спрощувати формули, задані в будь-якій формі, а не обов'язково в канонічній. У той же час ця операція не проходить, якщо члени, що породжують, містять різне входження (із запереченням і без нього) не однієї, а двох чи більше змінних. Наприклад,
про що, звичайно, не так просто догадатися на самому початку перетворення. Варто помітити, що з застосуванням узагальненого склеювання можна спрощувати формули, задані в будь-якій формі, а не обов'язково в канонічній. У той же час ця операція не проходить, якщо члени, що породжують, містять різне входження (із запереченням і без нього) не однієї, а двох чи більше змінних. Наприклад, 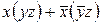 , тому що при цьому додатковий член
, тому що при цьому додатковий член 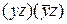 звертається в тотожний нуль.
звертається в тотожний нуль.
Хоча в розглянутому прикладі отримані мінімальні форми, у загальному випадку процедура склеювання мінтермів не гарантує цього. Вона забезпечує лише перетворення до скороченої форми, мінтерми якої називають простими імплікантами. Тому що що склеюються мінтерми покриваються мінтермом нижчого рангу, скорочена форма не містить таких імплікант, що цілком покриваються який-небудь однієї імплікантой. У той же час серед простих імплікант можуть бути такі, котрі покриваються сукупностями інших імплікант і, отже, є надлишковими. Після видалення надлишкових імплікант приходимо до тупикових форм, серед яких знаходяться і мінімальні форми. Варто зауважити, що для даної функції існує єдина скорочена форма, у той час як тупикових і мінімальних форм може бути кілька.
Карти Карно
Карти Карно являють собою спеціально організовані таблиці відповідності, на яких зручно здійснюються операції склеювання при спрощенні функції на шляху до мінімальних форм. Стовпці і рядки таблиці відповідають усіляким наборам значень змінних, причому ці набори розташовані в такому порядку, що кожен наступний відрізняється від попереднього тільки однієї з змінних. Завдяки цьому сусідні комірки по горизонталі і вертикалі відрізняються значенням тільки однієї перемінної. Комірці, розташовані по краях таблиці, також вважаються сусідніми і мають цю властивість. На рис. 3.2 показані карти Карно для двох, трьох і чотирьох змінних.
 Кожному набору значень змінних по рядках і стовпцям відповідає свій комірка, розташована на їхньому перетинанні. Вона заповнюється одиницею, якщо на відповідному наборі функція приймає одиничне значення, чи нулем при нульовому значенні функції (нулі звичайно не вписуються, а залишаються порожні комірки). Таким чином, відзначені комірки відповідають мінтермам, а невідмічені - макстермам канонічних форм. Наприклад, на рис. 3.3,а показана карта Карно для функції, заданою таблицею відповідності
Кожному набору значень змінних по рядках і стовпцям відповідає свій комірка, розташована на їхньому перетинанні. Вона заповнюється одиницею, якщо на відповідному наборі функція приймає одиничне значення, чи нулем при нульовому значенні функції (нулі звичайно не вписуються, а залишаються порожні комірки). Таким чином, відзначені комірки відповідають мінтермам, а невідмічені - макстермам канонічних форм. Наприклад, на рис. 3.3,а показана карта Карно для функції, заданою таблицею відповідності
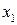
| |
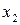
| |
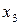
| |
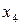
| |
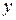
|
Операції склеювання двох мінтермів 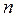 -го рангу вихідної, формули відповідає на карті Карно об'єднання двох сусідніх комірок, відзначених одиницями, і ця об'єднана пара комірок являє собою результуючий мінтерм
-го рангу вихідної, формули відповідає на карті Карно об'єднання двох сусідніх комірок, відзначених одиницями, і ця об'єднана пара комірок являє собою результуючий мінтерм 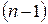 -го рангу. Аналогічне склеювання двох мінтермів
-го рангу. Аналогічне склеювання двох мінтермів 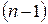 -го рангу в мінтерм
-го рангу в мінтерм 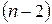 -го рангу представляється об'єднанням відповідних пар комірок у прямокутну групу з чотирьох сусідніх комірок і т.д. Повне число комірок у будь-якій групі завжди виражається цілим ступенем двійки
-го рангу представляється об'єднанням відповідних пар комірок у прямокутну групу з чотирьох сусідніх комірок і т.д. Повне число комірок у будь-якій групі завжди виражається цілим ступенем двійки 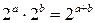 , де
, де 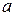 і
і 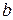 - відповідно цілі числа пар комірок по горизонталі і вертикалі, причому кожна така група відображає мінтерм
- відповідно цілі числа пар комірок по горизонталі і вертикалі, причому кожна така група відображає мінтерм 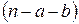 -ro рангу і покриває
-ro рангу і покриває 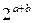 мінтермів
мінтермів 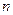 -го рангу вихідної канонічної форми. Так, на рис. 3.2,б показане скорочене покриття, імпліканти якого утворені в результаті склеювання мінтермів функції, зображеної на рис. 3.3, а. На рис. 3.3, в-е показані тупикові покриття розглянутої функції, причому покриття на рис. 3.3,в є мінімальним.
-го рангу вихідної канонічної форми. Так, на рис. 3.2,б показане скорочене покриття, імпліканти якого утворені в результаті склеювання мінтермів функції, зображеної на рис. 3.3, а. На рис. 3.3, в-е показані тупикові покриття розглянутої функції, причому покриття на рис. 3.3,в є мінімальним.
Зчитування мінтермів з карти Карно здійснюється послідовним розглядом груп комірок. У мінтерм входять тільки ті змінні, котрі зберігають свої значення в даній групі, причому значенням 1 відповідає сама змінна, а значенню 0 - її заперечення. Змінні, котрі приймають у даній групі різні значення (0 і 1), є вільними й у даному мінтермі відсутні. Приклади зчитування мінтермів з карт Карно для різного числа змінних показані на рис. 3.4.
|

 Будь-яка сукупність груп комірок, що покриває усі відзначені комірки, відповідає деякій сумі мінтермів різних рангів, що рівнозначна даної функції. Прагнення до найпростішої форми інтуїтивно розуміється як пошук такого мінімального покриття, число груп у який було б поменше, а самі групи були крупніше. Дійсно, чим менше груп у покритті, тим менше мінтермів у формулі, а при збільшенні розмірів групи відповідно знижується ранг мінтерму, а виходить, зменшується кількість змінних що в ньому вміщується. Практично для відшукання мінімального покриття на карті Карно насамперед вибирається відзначена комірка, що входить у таку найбільшу групу, що покриває будь-які інші можливі групи з цією коміркою. Після формування цієї найбільшої групи по тій же ознаці вибирається інша ще не покрита комірка і формується її найбільша група. Цей процес продовжується до тих пір, поки усі відзначені комірки виявляться, у тих чи інших групах або залишаться тільки такі непокриті комірки, які можна згрупувати різними способами. З можливих варіантів вибираються ті, котрі приводять до мінімальних покритів. Так для наведеного прикладу логічна функція буде мати вигляд
Будь-яка сукупність груп комірок, що покриває усі відзначені комірки, відповідає деякій сумі мінтермів різних рангів, що рівнозначна даної функції. Прагнення до найпростішої форми інтуїтивно розуміється як пошук такого мінімального покриття, число груп у який було б поменше, а самі групи були крупніше. Дійсно, чим менше груп у покритті, тим менше мінтермів у формулі, а при збільшенні розмірів групи відповідно знижується ранг мінтерму, а виходить, зменшується кількість змінних що в ньому вміщується. Практично для відшукання мінімального покриття на карті Карно насамперед вибирається відзначена комірка, що входить у таку найбільшу групу, що покриває будь-які інші можливі групи з цією коміркою. Після формування цієї найбільшої групи по тій же ознаці вибирається інша ще не покрита комірка і формується її найбільша група. Цей процес продовжується до тих пір, поки усі відзначені комірки виявляться, у тих чи інших групах або залишаться тільки такі непокриті комірки, які можна згрупувати різними способами. З можливих варіантів вибираються ті, котрі приводять до мінімальних покритів. Так для наведеного прикладу логічна функція буде мати вигляд 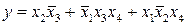 .
.
Для отримання мінімальної форми інверсії функції необхідно знайти на карті Карно мінімальне покриття сукупності нульових комірок і описати відповідну формулу за вище наведеним правилом. Так для функції на рис. 3.3, а є два таких покриття (рис.3.5), що відрізняються тільки однією імплікантою. Якщо необхідно знайти мінімальну форму як для добутку макстерім, то згідно принципу дуальності у виразі для інверсної функції достатньо замінити усі логічні операції на дуальні, а входження змінних на інверсні:
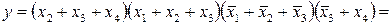
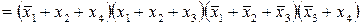 .
.
Ці ж форми можна записати на основі принципу дуальності безпосередньо по мінімальним покриттям нульових комірок карти Карно. Для цього достатньо кожну групу комірок ідентифікувати як суму змінних при інверсній розмітці карти Карно. , тобто відмічені значення змінних нульовими.
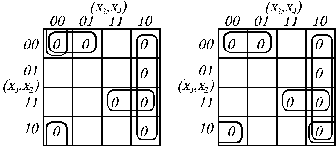
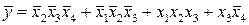
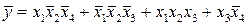
Рис. 3.5
Перехід від бульової функції до логічної схеми в бульовому базисі очевидний: досить відповідно до формули позначити входи вентилів і з'єднати їх між собою належним чином. Так, на рис. 3.6 показані логічні схеми, що реалізують мінімальні форми, отримані в наведених вище прикладах.
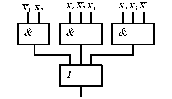
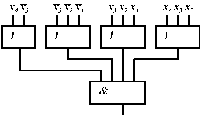
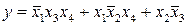
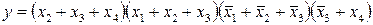
Рис. 3.6
Функції, задані в нормальної диз‘юнктивній чи кон‘юнктивній формі, реалізуються двоступінчастими схемами. Перша ступінь реалізує добутки чи суми змінних, а друга - відповідно суми мінтермів чи добутки макстермів. Двоступінчасті схеми кращі по швидкодії, що внаслідок інерційності логічних вентилів пропорційна числу ступеней.
Дата добавления: 2015-05-26; просмотров: 1188;

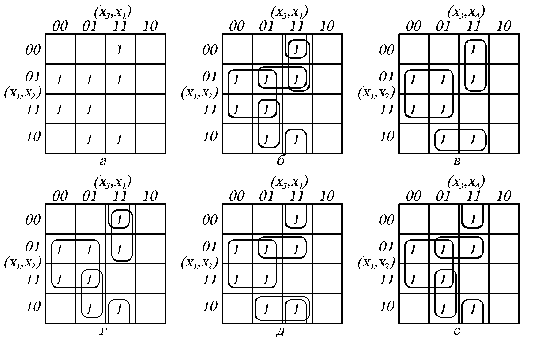 Рис. 3.3.
Рис. 3.3.