Теоретичні відомості і методичні вказівки. Перетворювачі кодів, шифратори, дешифратори
Перетворювачі кодів, шифратори, дешифратори
Функціональні вузли комбінаційного типу характеризуються однозначною відповідністю вихідних сигналів припустимим комбінаціям сигналів на вході і не залежать від послідовності їхньої зміни. Для побудови комбінаційного функціонального вузла повинна бути задана вся безліч кодів (слів) і відповідний їм набір вихідних кодів або система рівнянь, що описує залежність кожного розряду вихідного коду від незалежних вхідних змінних. Комбінаційні схеми будуються або на основі логічних елементів, або на основі постійних запам'ятовуючих пристроїв (ПЗП), у які записується таблиця перетворення вхідних слів у вихідні. До комбінаційних функціональних вузлів відносяться перетворювачі кодів, (частковим випадком яких є шифратори і дешифратори), мультіплексори, демультіплексори, пристрої зсуву чисел, комбінаційні суматори, цифрові компаратори та ін.
Перетворювачі кодів призначені для переведення чисел з однієї форми представлення в іншу. Наприклад, при введенні інформації в ЕОМ необхідно перетворювати десяткові числа в двійкові, а при виведенні інформації на індикатори чи друкувальний пристрій - двійкові або двійково-десяткові коди в коди керування знакогенератором, світлодиодними чи рідиннокрісталічними індикаторними панелями.
Відправним пунктом для побудови перетворювача кодів є таблиця відповідності, у якій записується повний набір вхідних і відповідний набір вихідних слів. Якщо вхідні і вихідні слова записані двійковими символами, то синтез перетворювача коду зводиться до перебування для кожного розряду вихідного слова бульової функції, що встановлює зв'язок даного розряду з вхідними наборами двійкових змінних. Організація такого зв'язку і мінімізація бульового виразу здійснюються за допомогою карт Карно (діаграм Вейча). На заключному етапі отримана функція перетвориться до виду, зручному для реалізації в заданому (обраному) елементному базисі.
Як приклад розглянемо спосіб візуалізації двійково-десяткових чисел, якій часто проводять за допомогою семісегментних панелей на основі рідких кристалів чи світлодіодів (рис. 3.13,а), широко використовуваних у мікрокалькуляторах, електронних годинниках і т.д. Якщо сегменти позначені буквами, як показано на рис. 3.13,б, то табл. 3.4 встановлює відповідність між двійково-десятковим числом і необхідними для відображення десяткової цифри набором сегментів.
Таблиця 3.4 Таблиця 3.5
| Десяткове число | Код 8421 DCBA | Семісегментний код abcdefg | Десяткове число | Вхідний код
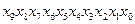
| Код 8421
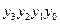
| |
| * | 0 0 0 0 0 0 0 0 0 0 | 0 0 0 0 | ||||
| 0 0 0 0 0 0 0 0 0 1 | 0 0 0 0 | |||||
| 0 0 0 0 0 0 0 0 1 0 | 0 0 0 1 | |||||
| 0 0 0 0 0 0 0 1 0 0 | 0 0 1 0 | |||||
| 0 0 0 0 0 0 1 0 0 0 | 0 0 1 1 | |||||
| 0 0 0 0 0 1 0 0 0 0 | 0 1 0 0 | |||||
| 0 0 0 0 1 0 0 0 0 0 | 0 1 0 1 | |||||
| 0 0 0 1 0 0 0 0 0 0 | 0 1 1 0 | |||||
| 0 0 1 0 0 0 0 0 0 0 | 0 1 1 1 | |||||
| 0 1 0 0 0 0 0 0 0 0 | 1 0 0 0 | |||||
| 1 0 0 0 0 0 0 0 0 0 | 1 0 0 1 |
Сегмент 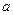 визначається наборами коду 8421 у такий спосіб:
визначається наборами коду 8421 у такий спосіб:
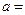
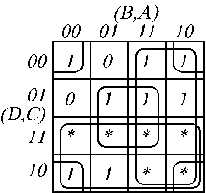
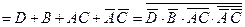
Аналогічно одержимо бульові вирази для інших сегментів:
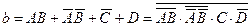 ;
;
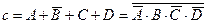 ;
;
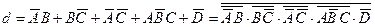 ;
;
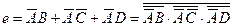
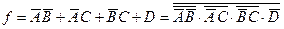 ;
;
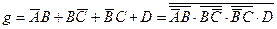 .
.
 Схема перетворювача коду 8421 у код семісегментного індикатора, реалізована на елементах І-НІ, показана на рис. 3.14.
Схема перетворювача коду 8421 у код семісегментного індикатора, реалізована на елементах І-НІ, показана на рис. 3.14.
Частковим випадком перетворювача кодів є шифратор - пристрій, що забезпечує видачу визначеного коду у відповідь на сигнал одного з входів. Шифратори широко використовуються для перетворення десяткових цифр і буквених символів у двійковий код при введенні інформації в ЕОМ і інші цифрові пристрої.
 Розглянемо приклад побудови шифратора для перетворення десяткових чисел у код 8421 згідно табл. 3.5. Вхідними є двійкові змінні
Розглянемо приклад побудови шифратора для перетворення десяткових чисел у код 8421 згідно табл. 3.5. Вхідними є двійкові змінні 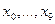 , котрі формуються при натисканні відповідної клавіші пристрою введення. Змінні є незалежними і дозволяють побудувати
, котрі формуються при натисканні відповідної клавіші пристрою введення. Змінні є незалежними і дозволяють побудувати 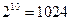 вхідних комбінацій, але якщо накладається обмеження, що забороняє натискання двох і більш клавіш, то з 1024 залишається 11 припустимих вхідних комбінацій. Відповідний даному обмеженню вхідний код називають кодом «1 з
вхідних комбінацій, але якщо накладається обмеження, що забороняє натискання двох і більш клавіш, то з 1024 залишається 11 припустимих вхідних комбінацій. Відповідний даному обмеженню вхідний код називають кодом «1 з 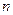 » чи унітарним. У табл. 3.5 натиснутій клавіші відповідає «логічна 1», а ненатиснутій - «логічний 0». Дві перших вхідних комбінації породжують той самий двійковий код 0000. Відмінність між ними полягає в тому, що при натисканні клавіші «0», як і при введенні інших цифр, у пристрої повинна формуватися команда введення і запам'ятовування чергової десяткової цифри. Як видно з табл. 3.5, двійкова змінна
» чи унітарним. У табл. 3.5 натиснутій клавіші відповідає «логічна 1», а ненатиснутій - «логічний 0». Дві перших вхідних комбінації породжують той самий двійковий код 0000. Відмінність між ними полягає в тому, що при натисканні клавіші «0», як і при введенні інших цифр, у пристрої повинна формуватися команда введення і запам'ятовування чергової десяткової цифри. Як видно з табл. 3.5, двійкова змінна 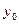 приймає значення «1», якщо «1» з'являється на
приймає значення «1», якщо «1» з'являється на 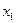 чи вході на вході
чи вході на вході 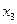 , чи
, чи 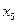 , чи
, чи 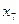 , чи
, чи  . При всіх інших вхідних комбінаціях
. При всіх інших вхідних комбінаціях 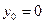 , тобто в термінах алгебри логіки
, тобто в термінах алгебри логіки
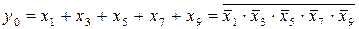 . (3.1 а)
. (3.1 а)
Аналогічно запишемо для інших входів:
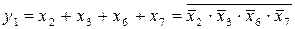 , (3.1 б)
, (3.1 б)
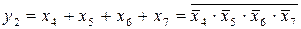 , (3.1 в)
, (3.1 в)
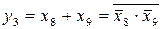 . (3.1 г)
. (3.1 г)
Відповідно до приведених рівностей (3.1) шифратор можна реалізувати в базисі АБО-НІ (рис. 3.15,а, б) або в базисі І-НІ (рис.3.15,в, г).
 |
Зворотне перетворення двійкового коду в код «1 з
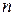 » виконують перетворювачі коду, називані дешифраторами. Найбільше широко дешифратори використовуються в пристроях виведення інформації з ЕОМ і інших цифрових пристроїв на зовнішні пристрої візуалізації і документування алфавітно-цифрової інформації. Для цього потрібно подати сигнал на 1 з
» виконують перетворювачі коду, називані дешифраторами. Найбільше широко дешифратори використовуються в пристроях виведення інформації з ЕОМ і інших цифрових пристроїв на зовнішні пристрої візуалізації і документування алфавітно-цифрової інформації. Для цього потрібно подати сигнал на 1 з 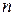 , наприклад, катодів газорозрядного індикатора чи елементів вибірки символів друкуючого пристрою.
, наприклад, катодів газорозрядного індикатора чи елементів вибірки символів друкуючого пристрою.
Таблиця 3.6 Таблиця 3.7
Вхідний
код 21
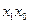
| Вихідний код «1 з 4»
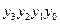
| Вихідний код 8421
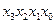
| Вихідний код «1 з 10»
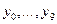
| |
| 0 0 | 0 0 0 1 | 0 0 0 0 | 1 0 0 0 0 0 0 0 0 0 | |
| 0 1 | 0 0 1 0 | 0 0 0 1 | 0 1 0 0 0 0 0 0 0 0 | |
| 1 0 | 0 1 0 0 | 0 0 1 0 | 0 0 1 0 0 0 0 0 0 0 | |
| 1 0 0 0 | 0 0 1 1 | 0 0 0 1 0 0 0 0 0 0 | ||
| 0 1 0 0 | 0 0 0 0 1 0 0 0 0 0 | |||
| 0 1 0 1 | 0 0 0 0 0 1 0 0 0 0 | |||
| 0 1 1 0 | 0 0 0 0 0 0 1 0 0 0 | |||
| 0 1 1 1 | 0 0 0 0 0 0 0 1 0 0 | |||
| 1 0 0 0 | 0 0 0 0 0 0 0 0 1 0 | |||
| 1 0 0 1 | 0 0 0 0 0 0 0 0 0 1 |
Синтез структури дешифратора, як і будь-якого іншого перетворювача кодів, починається з запису таблиці відповідності вхідних і вихідних кодів. Нехай необхідно перетворити двійковий код 21 у код «1 з 4». Тоді табл. 3.6 цілком визначає значення виходів для усіх вхідних наборів. Далі випливає для кожної вихідної функції скласти карту Карно і одержати її мінімізований вираз. У розглянутому прикладі у цьому намає сенсу, тому що для кожної функції 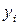 карта Карно містить тільки одну «1», тому відповідний їй мінтерм і є мінімальною формою. Тоді на підставі табл. 3.7 запишемо:
карта Карно містить тільки одну «1», тому відповідний їй мінтерм і є мінімальною формою. Тоді на підставі табл. 3.7 запишемо:
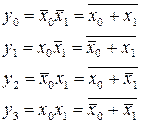 (3.2)
(3.2)
 |
Вираз (3.2) можна реалізувати в елементному базисі І-НІ (рис. 3.16,а, б) або базисі АБО-НІ (рис. 3.16,в).
Якщо число входів 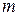 і число виходів
і число виходів 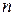 дешифратора зв'язані співвідношенням
дешифратора зв'язані співвідношенням 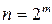 , то виходи визначені для всіх двійкових наборів і дешифратор називається повним. У випадку
, то виходи визначені для всіх двійкових наборів і дешифратор називається повним. У випадку 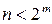 дешифратор називається неповним. Приклад неповного дешифратора - перетворювач двійкового коду 8421 у код «1 з 10» згідно табл. 3.7.
дешифратор називається неповним. Приклад неповного дешифратора - перетворювач двійкового коду 8421 у код «1 з 10» згідно табл. 3.7.
Оскільки 6 з 16 можливих вхідних наборів не визначені, мається можливість довільним довизначенням карти Карно мінімізувати ряд вихідних функцій дешифратора. Наприклад, функції 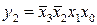 і
і 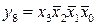 можна спростити до виду:
можна спростити до виду:
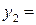
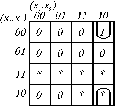
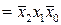 ,
, 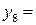
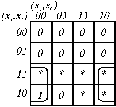
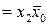
Аналогічно спрощуються функції 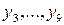 . З огляду на те що функції
. З огляду на те що функції 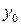 і
і 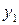 не спрощуються, у чому легко можна переконатися, побудувавши для них карти Карно, остаточно запишемо логічні функції, що повинний реалізувати синтезований десятковий дешифратор:
не спрощуються, у чому легко можна переконатися, побудувавши для них карти Карно, остаточно запишемо логічні функції, що повинний реалізувати синтезований десятковий дешифратор:
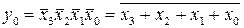 ;
;
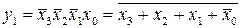 ;
;
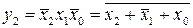 ;
;
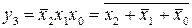 ;
;
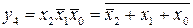 ;
;
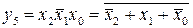 ;
;
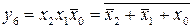 ;
;
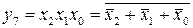 ;
;
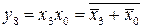 ;
;
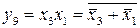 .
.
 |
Відповідний десятковий дешифратор реалізований на основі логічних елементів АБО-НІ (рис. 3.17). Відзначимо, що в мінімізованому варіанті дешифратора не допускається подача на його вхід кодів 8421, що не ввійшли в табл. 3.7. Так, якщо на вхід дешифратора на рис. 3.17 подать код 1011, то одночасно на двох виходах
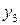 і
і 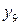 встановлюються «логічні 1». Таким чином, якщо на входах дешифратора можуть подаватися будь-які з
встановлюються «логічні 1». Таким чином, якщо на входах дешифратора можуть подаватися будь-які з 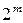 комбінацій і не допускається одночасне збудження більш ніж одного з його
комбінацій і не допускається одночасне збудження більш ніж одного з його 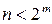 виходів, спрощення схеми описаним методом неприпустимо і кожна з вихідних функцій повинна бути визначена повним набором вхідних змінних. У такому неповному дешифраторі (як приклад на рис. 3.18 показаний варіант на елементах І-НІ) «зайві» вхідні комбінації не збуджують жоден з його виходів:
виходів, спрощення схеми описаним методом неприпустимо і кожна з вихідних функцій повинна бути визначена повним набором вхідних змінних. У такому неповному дешифраторі (як приклад на рис. 3.18 показаний варіант на елементах І-НІ) «зайві» вхідні комбінації не збуджують жоден з його виходів: 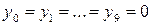 .
.
Мультіплексори і демультіплексори
У цифрових пристроях часто виникає задача передачі цифровий, інформації від 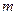 різних пристроїв до
різних пристроїв до 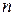 приймачів через канал загального користування. Для цього на вході каналу встановлюється пристрій, називане мультіплексором, що відповідно до коду адреси
приймачів через канал загального користування. Для цього на вході каналу встановлюється пристрій, називане мультіплексором, що відповідно до коду адреси 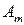 підключає до каналу одне з джерел інформації, а на виході каналу пристрій демультіплексор забезпечує передачу інформації до приймача, що має цифрову адресу
підключає до каналу одне з джерел інформації, а на виході каналу пристрій демультіплексор забезпечує передачу інформації до приймача, що має цифрову адресу 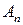 . Мультіплексор і демультіплексор містять у собі дешифратор адреси. Сигнали дешифратора керують логічними вентилями, дозволяючи передачу інформації тільки через один з них. Логіка функціонування мультіплексора для
. Мультіплексор і демультіплексор містять у собі дешифратор адреси. Сигнали дешифратора керують логічними вентилями, дозволяючи передачу інформації тільки через один з них. Логіка функціонування мультіплексора для 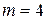 описується табл. 3.8, де
описується табл. 3.8, де 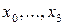 - виходи незалежних джерел інформації. Логіку функціонування демультіплексора для випадку
- виходи незалежних джерел інформації. Логіку функціонування демультіплексора для випадку 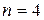 ілюструються табл. 3.9, де
ілюструються табл. 3.9, де 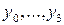 - входи приймачів інформації.
- входи приймачів інформації.
Найпростіший мультіплексор, що реалізує задане табл. 3.8 перетворення, можна побудувати на логічних елементах І, АБО і лінійному дешифраторі (рис. 3.19,а). У такій структурі вихід мультіплексора 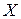 встановлюється з затримкою адресних сигналів у трьох логічних ступенях. Швидкодія мультіплексора можна збільшити, якщо сполучити дешифратор адреси й інформаційні вентилі (рис. 3.19,б). Вхід
встановлюється з затримкою адресних сигналів у трьох логічних ступенях. Швидкодія мультіплексора можна збільшити, якщо сполучити дешифратор адреси й інформаційні вентилі (рис. 3.19,б). Вхід 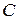 (рис. 3.19,в) забезпечує передачу інформації в канал тільки в дозволені строб-імпульсом моменти часу.
(рис. 3.19,в) забезпечує передачу інформації в канал тільки в дозволені строб-імпульсом моменти часу.
Таблиця 3.8 Таблиця 3.9
| Вхід | Адреса
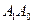
| Вихід
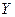
| Вхід | Адреса
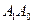
| Вихід
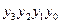
| |
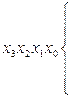
| 0 0 | 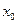
| 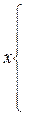
| 0 0 | 0 0 0 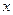
| |
| 0 1 | 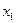
| 0 1 | 0 0 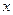 0 0
| |||
| 1 0 | 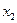
| 1 0 | 0 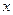 0 0 0 0
| |||
| 1 1 | 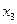
| 1 1 | 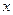 0 0 0 0 0 0
|
Аналогічно можна побудувати демультіплексори (рис. 3.20,а, б, в) відповідно до табл. 3.9.
Комбінаційні суматори
Суматор - пристрій, призначений для виконання операцій додавання і віднімання багаторозрядних чисел (операндів). Багаторозрядний суматор складається з однорозрядних, що реалізують додавання однорозрядних чисел. Однорозрядний суматор, на вхід якого надходять два однорозрядних числа 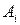 і
і 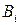 , а на виході формуються також однорозрядні числа суми
, а на виході формуються також однорозрядні числа суми 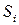 і переносу
і переносу 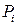 , називають напівсуматором (рис. 3.21,а). Якщо однорозрядний суматор реалізує додавання трьох однорозрядних чисел
, називають напівсуматором (рис. 3.21,а). Якщо однорозрядний суматор реалізує додавання трьох однорозрядних чисел 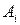 ,
, 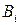 і
і 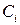 (перенос з молодшого розряду), то такий суматор називають повним. У багаторозрядному суматорі тільки самий молодший розряд можна виконати за схемою напівсуматора, а інші розряди виконують функції повного суматора. Нижче розглянуті схеми суматорів для двійково-кодованих чисел.
(перенос з молодшого розряду), то такий суматор називають повним. У багаторозрядному суматорі тільки самий молодший розряд можна виконати за схемою напівсуматора, а інші розряди виконують функції повного суматора. Нижче розглянуті схеми суматорів для двійково-кодованих чисел.
 |
Таблиця відповідності для напівсуматора (табл. 3.10) дозволяє записати функцію обчислення суми
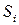 і переносу одиниці переповнення
і переносу одиниці переповнення 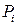 в старший розряд:
в старший розряд:
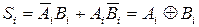 ;
;
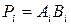 . (3.3)
. (3.3)
Відповідно до виразів (3.3) напівсуматор можна реалізувати в базисі елементів І-НІ (рис.3.21,б), АБО-НІ або на основі логічного, елемента ВИКЛЮЧНЕ АБО і кон‘юнктора (рис. 3.21,в).
 |
 Вибір схеми для реалізації напівсуматора визначається наявною в розпорядженні розробника елементною базою з урахуванням вимог по швидкодії, енергоспоживанню і технологічності. Для забезпечення максимальної швидкодії більш прийнятні схеми з мінімальною кількістю логічних ступенів між входом і виходом. З цього погляду удавана простота напівсуматора на рис. 3.21, в не дає очікуваної переваги по швидкодії, тому що внутрішня структура ІМС ВИКЛЮЧНЕ АБО власне кажучи повторює фрагмент схеми на рис. 3.21,б.
Вибір схеми для реалізації напівсуматора визначається наявною в розпорядженні розробника елементною базою з урахуванням вимог по швидкодії, енергоспоживанню і технологічності. Для забезпечення максимальної швидкодії більш прийнятні схеми з мінімальною кількістю логічних ступенів між входом і виходом. З цього погляду удавана простота напівсуматора на рис. 3.21, в не дає очікуваної переваги по швидкодії, тому що внутрішня структура ІМС ВИКЛЮЧНЕ АБО власне кажучи повторює фрагмент схеми на рис. 3.21,б.
 Суттєвим недоліком напівсуматора є те, що він не враховує сигнал переносу з старшого розряду. Для того що враховувати для знаходження сигнали переносу з старшого розряду використовують схему повного суматора (рис. 3.22).
Суттєвим недоліком напівсуматора є те, що він не враховує сигнал переносу з старшого розряду. Для того що враховувати для знаходження сигнали переносу з старшого розряду використовують схему повного суматора (рис. 3.22).
Робота повного суматора описується табл. 3.11.
Карта Карно для функцій 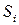 і дає мінімальну форму і її тотожні варіанти:
і дає мінімальну форму і її тотожні варіанти:
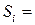

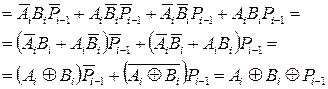 (3.4)
(3.4)
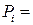
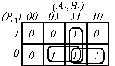
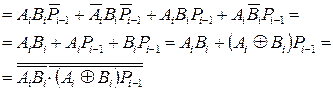 (3.5)
(3.5)
 Відповідно до виразів (3.4), (3.5) на рис. 3.23 наведена реалізація повного суматора і його умовне графічне зображення.
Відповідно до виразів (3.4), (3.5) на рис. 3.23 наведена реалізація повного суматора і його умовне графічне зображення.
Аналогічно визначимо функції переключення повного віднімача (називаного також субтрактором) - пристрою, що реалізує операцію віднімання двох однорозрядних чисел з формуванням сигналу зайому зі старшого розряду. Відповідно до таблиці істинності віднімача (табл. 3.12), (рис. 3.24) запишемо вираз для різниці 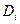 і функції зайому
і функції зайому 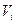 :
:
 |
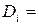

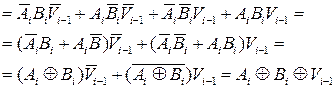 (3.6)
(3.6)
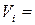
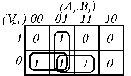
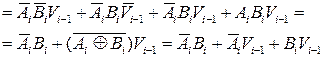 (3.7)
(3.7)
 Порівнюючи вирази для суми
Порівнюючи вирази для суми 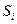 і переносу
і переносу 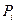 повного суматора з виразами для різниці
повного суматора з виразами для різниці 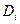 і заема
і заема 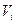 віднімача, бачимо, що вираз для
віднімача, бачимо, що вираз для 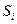 й
й 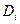 ідентичні, а для
ідентичні, а для 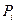 і
і 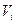 - відрізняються. Якщо у виразу
- відрізняються. Якщо у виразу 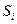 і
і 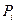 замість
замість 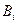 підставити
підставити 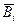 , а замість
, а замість 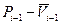 те
те 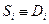 ;
; 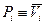 . Це означає, що віднімання можна замінити підсумовуванням, представивши від'ємник у зворотному коді з урахуванням необхідної інверсії функції зайому. Це особливо важливо для побудови суматора, що виконує додавання чисел з довільними знаками. Якщо ж необхідно робити операцію тільки віднімання, можна використовувати схему на рис. 3.25. Схема на рис. 3.25 виконує операцію віднімання з затримкою сигналу в шости логічних ступенях. Її реалізанія виконана тільки на двовходових елементах І-НІ. У цьому випадку формування значення різниці
. Це означає, що віднімання можна замінити підсумовуванням, представивши від'ємник у зворотному коді з урахуванням необхідної інверсії функції зайому. Це особливо важливо для побудови суматора, що виконує додавання чисел з довільними знаками. Якщо ж необхідно робити операцію тільки віднімання, можна використовувати схему на рис. 3.25. Схема на рис. 3.25 виконує операцію віднімання з затримкою сигналу в шости логічних ступенях. Її реалізанія виконана тільки на двовходових елементах І-НІ. У цьому випадку формування значення різниці 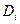 здійснюється відповідно до виразів (3.6), а зайому - (3.7).
здійснюється відповідно до виразів (3.6), а зайому - (3.7).
Сполучення операцій додавання і віднімання вимагає додаткового сигналу 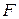 , що встановлює режим роботи суматора. У суматорі (рис. 3.26) при
, що встановлює режим роботи суматора. У суматорі (рис. 3.26) при 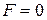 виробляються підсумовування чисел і формування переносу в наступний розряд, а при
виробляються підсумовування чисел і формування переносу в наступний розряд, а при 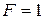 - віднімання
- віднімання 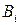 з
з 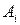 і формування зайому із старшого розряду.
і формування зайому із старшого розряду.
 |
Дата добавления: 2015-05-26; просмотров: 1510;
