Теоретичні відомості і методичні вказівки. Функції, задані в нормальної дизюнктивній чи конюнктивній формі, реалізуються дворівневими схемами
Функції, задані в нормальної дизюнктивній чи конюнктивній формі, реалізуються дворівневими схемами. Перший рівень реалізує добутки чи суми змінних, а друга - відповідно суми минтермів чи добутки макстермів. Дворівневі схеми кращі по швидкодії, що внаслідок інерційності логічних вентилів пропорційно числу рівней. Однак в інженерній практиці приходиться по різних причинах звертатися до багаторівневих схем.
Багаторівневі реалізації
Характерним прикладом багаторівневих схем може служити реалізація функції, що забезпечує перевірку на парність набору з змінних. Вона дорівнює одиниці тоді і тільки тоді, коли число одиничних значень вхідних змінних непарне і виражається як сума по модулі 2: 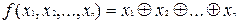 . Реалізація цієї функції дворівневою схемою при значному числі
. Реалізація цієї функції дворівневою схемою при значному числі 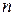 нереальна, тому що треба було б
нереальна, тому що треба було б 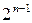 вентилів І на
вентилів І на 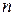 входів кожен і один вентиль АБО на
входів кожен і один вентиль АБО на 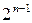 входів. Це випливає з того, що серед
входів. Це випливає з того, що серед 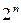 наборів значень змінних завжди половина непарних, і канонічна форма функції містить
наборів значень змінних завжди половина непарних, і канонічна форма функції містить 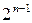 мінтермів. До того ж вона не мінімізується, тому що не містить ні однієї пари мінтермів що склеюються (на карті Карно відзначені комірки розташовуються в шаховому порядку). У той же час дана функція реалізується багаторівневою схемою, що складається з двовходових вентилів виключне АБО, що виконують операцію сума по модулю 2, причому для функції
мінтермів. До того ж вона не мінімізується, тому що не містить ні однієї пари мінтермів що склеюються (на карті Карно відзначені комірки розташовуються в шаховому порядку). У той же час дана функція реалізується багаторівневою схемою, що складається з двовходових вентилів виключне АБО, що виконують операцію сума по модулю 2, причому для функції 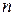 змінних таких вентилів потрібно (
змінних таких вентилів потрібно ( 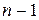 ). Відповідна схема при
). Відповідна схема при 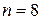 показана на рис. 3.7,а. Реалізація в булевом базисі вимагає заміни вентилів виключне АБО що відповідають булевими еквівалентами - диз'юнктивними (рис. 3.7,6) чи кон'юнктивними (рис. 3.7,в). В результаті функція реалізується двовходовими вентилями І і АБО разом з вентилями НІ, причому усего потрібно
показана на рис. 3.7,а. Реалізація в булевом базисі вимагає заміни вентилів виключне АБО що відповідають булевими еквівалентами - диз'юнктивними (рис. 3.7,6) чи кон'юнктивними (рис. 3.7,в). В результаті функція реалізується двовходовими вентилями І і АБО разом з вентилями НІ, причому усего потрібно 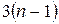 логічних вентилів і
логічних вентилів і 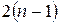
 інверторів.
інверторів.
 |  |
Багатоступінчасті реалізації з'являються також внаслідок перетворень стандартних форм, викликаних практичними обмеженнями по числу входів вентиля (коефіцієнту розгалуження) і числу виходів (коефіцієнту занурення). В одному зі способів зменшення числа входів досягається розкладанням бульової формули на множники. Наприклад, функція
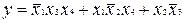 , двоступінчаста реалізація якої показана на рис.3.6, перетвориться до виду:
, двоступінчаста реалізація якої показана на рис.3.6, перетвориться до виду: 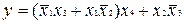 . Відповідна багатоступінчаста реалізація, у якій використовуються тільки двовходові вентилі, показана на рис. 3.8. Будь-які обмеження на коефіцієнти розгалуження і навантаження можна задовольнити заміною вентилів з неприпустимо великим числом входів і виходів так називаними деревоподібними схемами (рис. 3.9). Одна з таких схем уже використовувалася вище для реалізації функції перевірки на парність. Вентиль на
. Відповідна багатоступінчаста реалізація, у якій використовуються тільки двовходові вентилі, показана на рис. 3.8. Будь-які обмеження на коефіцієнти розгалуження і навантаження можна задовольнити заміною вентилів з неприпустимо великим числом входів і виходів так називаними деревоподібними схемами (рис. 3.9). Одна з таких схем уже використовувалася вище для реалізації функції перевірки на парність. Вентиль на 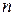 входів реалізується деревоподібною схемою, що складається з (
входів реалізується деревоподібною схемою, що складається з ( 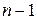 ) двовходових вентилів, причому число ступіней дорівнює
) двовходових вентилів, причому число ступіней дорівнює 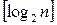 , тобто найменшому цілому числу, більшому чи рівний
, тобто найменшому цілому числу, більшому чи рівний 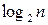 (рис. 3.9,а). Аналогічно вентиль з виходами реалізується деревоподібною схемою, що містить також
(рис. 3.9,а). Аналогічно вентиль з виходами реалізується деревоподібною схемою, що містить також 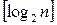 ступіней, а кожен вентиль має один вхід і два виходи (рис. 3.9,6).
ступіней, а кожен вентиль має один вхід і два виходи (рис. 3.9,6).
Факторизація
У загальному випадку врахування реальних обмежень на навантажувальні здібності джерел вхідних і внутрішніх змінних і на коефіцієнти розгалуження кон‘юнкторів передує синтезу логічної схеми в бульовому базисі і називається факторизацією. Цей процес формалізується за допомогою таблиці импликант 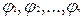 , що покривають дану функцію і відповідають мінтермам диз'юнктивної нормальної форми
, що покривають дану функцію і відповідають мінтермам диз'юнктивної нормальної форми 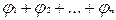 . Таблиця містить
. Таблиця містить 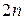 стовпців для змінних і їхніх інверсій, а також
стовпців для змінних і їхніх інверсій, а також 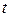 рядків для імплікант. Наприклад, для функції
рядків для імплікант. Наприклад, для функції 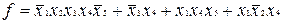 вона виглядає в такий спосіб:
вона виглядає в такий спосіб:

| 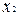
| 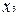
| 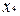
| 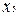
| 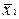
| 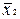
| 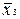
| 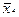
| 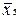
| |
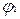
| ||||||||||
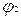
| ||||||||||
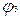
| ||||||||||
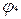
|
При заданому коефіцієнті нагружения 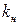 факторизації підлягають джерела змінних, що мають більше
факторизації підлягають джерела змінних, що мають більше 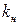 виходів. Для цього необхідно в таблиці імплікант зі стовпця факторизуємої змінної перенести по тим же рядкам надлишкові одиниці в додаткові стовпці так, щоб число одиниць у кожнім з них було не більше
виходів. Для цього необхідно в таблиці імплікант зі стовпця факторизуємої змінної перенести по тим же рядкам надлишкові одиниці в додаткові стовпці так, щоб число одиниць у кожнім з них було не більше 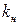 . Такі стовпці відповідають додатковим вентилям, що повинні бути зв'язані з даним джерелом. Для врахування цих зв'язків необхідно додати до таблиці відповідну кількість рядків і записати в них по стовпцю факторизуємої змінної одиниці. При
. Такі стовпці відповідають додатковим вентилям, що повинні бути зв'язані з даним джерелом. Для врахування цих зв'язків необхідно додати до таблиці відповідну кількість рядків і записати в них по стовпцю факторизуємої змінної одиниці. При 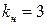 приведена вище таблиця перетвориться до виду:
приведена вище таблиця перетвориться до виду:

| 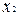
| 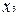
| 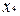
| 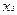
| 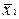
| 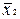
| 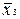
| 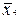
| 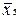
| 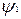
| |
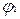
| |||||||||||
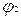
| |||||||||||
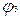
| |||||||||||
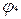
| |||||||||||
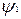
|
Тут зі стовпця 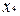 перенесені в додатковий стовпець
перенесені в додатковий стовпець 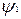 три одиниці і додано рядок
три одиниці і додано рядок 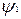 з одиницею в стовпці
з одиницею в стовпці 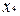 . Це відповідає перетворенню джерела змінної
. Це відповідає перетворенню джерела змінної 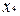 , як показано на рис. 3.10, а, де через
, як показано на рис. 3.10, а, де через 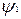 , позначений додатковий вентиль, що розмножує дану змінну
, позначений додатковий вентиль, що розмножує дану змінну 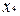 . Факторизація входів при заданому коефіцієнті розгалуження
. Факторизація входів при заданому коефіцієнті розгалуження 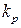 здійснюється аналогічно розподілом надлишкових одиниць по додаткових рядках. Так, у розглянутому прикладі при заданому
здійснюється аналогічно розподілом надлишкових одиниць по додаткових рядках. Так, у розглянутому прикладі при заданому 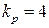 таблиця імплікант перетвориться до виду:
таблиця імплікант перетвориться до виду:

| 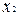
| 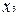
| 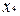
| 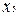
| 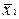
| 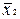
| 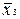
| 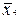
| 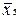
| 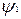
| 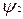
| |
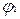
| ||||||||||||
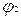
| ||||||||||||
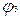
| ||||||||||||
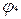
| ||||||||||||
| ||||||||||||
|
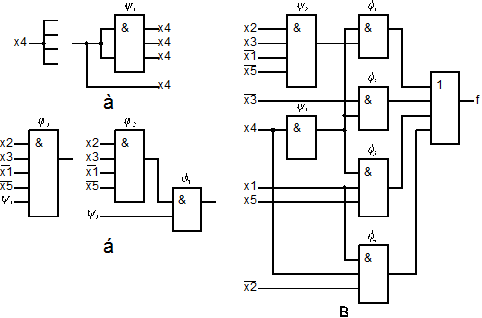
Рис. 3.10
 Тут з рядка
Тут з рядка 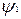 перенесені чотири одиниці в додатковий рядок
перенесені чотири одиниці в додатковий рядок 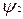 , а в першому рядку додаткового стовпця
, а в першому рядку додаткового стовпця 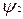 занесена одиниця. Це відповідає перетворенню вентиля з п'ятьма входами, як показано на рис. 3.10 б. Перетвореній таблиці відповідає комбінаційна схема, приведена на рис. 3.10.в. Інший варіант багатоступінчастої реалізації можна одержати за допомогою перетворення функції до скобкової форми:
занесена одиниця. Це відповідає перетворенню вентиля з п'ятьма входами, як показано на рис. 3.10 б. Перетвореній таблиці відповідає комбінаційна схема, приведена на рис. 3.10.в. Інший варіант багатоступінчастої реалізації можна одержати за допомогою перетворення функції до скобкової форми: 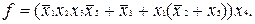
Базиси І-НІ та АБО-НІ
Внаслідок функціональної повноти функцій Шеффера і стрілки Пірса (див. табл. 3.2) реалізуючі їх вентилі І-НІ чи АБО-НІ можуть представляти будь-яку бульову операцію І, АБО, НІ і у такий спосіб самостійно утворити базис, у якому реалізується будь-яка логічна функція. Це доцільно з двох точок зору. По-перше, при проектуванні логічних схем можна обійтися одним єдиним типом вентиля, що дозволяє гранично уніфікувати цей процес. По-друге, для більшості серій ТТЛ- і КМОНП-логік вентиль І-НІ, як і АБО-НІ, є базисним і кращий у багатьох відносинах. Внаслідок цього реалізація логічних схем у базисах І-НІ і АБО-НІ одержала широке поширення в практиці.
Бульові операції І, АБО, НІ виражаються через штрих Шеффера 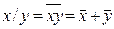 співвідношеннями
співвідношеннями 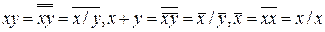
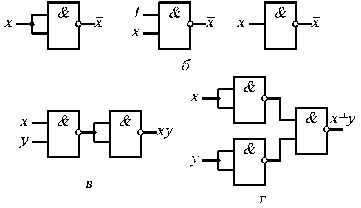
Рис. 3.11
Звідси випливає, що вентиль І-НІ, таблиця відповідності якого дана на рис.3.11,а, еквівалентний вентилю АБО-НІ (див. табл. 3.3) і дозволяє реалізувати бульові операції, як показано на рис. 3.11,б-г. Для реалізації інверсії маються два варіанти: або на усі входи вентиля І-НІ подається змінна 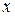 , або на усі входи, крім входу
, або на усі входи, крім входу 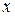 , подається одиниця. Звичайно ці особливості на схемах відсутні і використовується спрощене представлення з одним входом (рис. 3.11, б).
, подається одиниця. Звичайно ці особливості на схемах відсутні і використовується спрощене представлення з одним входом (рис. 3.11, б).
Перехід до базису І-НІ здійснюється простіше всього для дворівневих схем І/АБО чи при завданні функції в стандартній формі суми мінтермів, що видно на простому прикладі 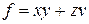 (рис. 3.12). Вихідна схема в булевом базисі (рис. 3.12, а) перетвориться до такого виду (рис. 3.12, б), що пари інверторів виявляються з'єднаними послідовно і виконують подвійну інверсію сигналів. Після їхнього видалення схема, а вентилями І-НІ істотно спрощується (рис. 3.12, в) і по своїй структурі цілком збігається з вихідною схемою. Таким чином, для переходу від дворівневої схеми І-АБО до схеми в базисі І-НІ досить замінити усі вентилі вентилями І-НІ.
(рис. 3.12). Вихідна схема в булевом базисі (рис. 3.12, а) перетвориться до такого виду (рис. 3.12, б), що пари інверторів виявляються з'єднаними послідовно і виконують подвійну інверсію сигналів. Після їхнього видалення схема, а вентилями І-НІ істотно спрощується (рис. 3.12, в) і по своїй структурі цілком збігається з вихідною схемою. Таким чином, для переходу від дворівневої схеми І-АБО до схеми в базисі І-НІ досить замінити усі вентилі вентилями І-НІ.
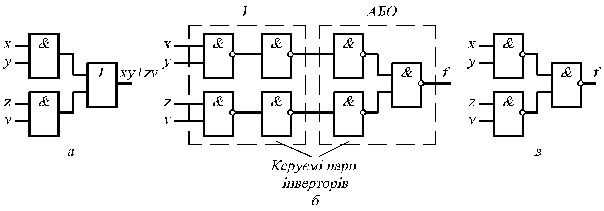
Рис. 3.12.
Дата добавления: 2015-05-26; просмотров: 753;
