Теоретичні відомості і методичні вказівки. Параметри цифрових елементів поділяють на експлуатаційні, економічні, технічні
Параметри цифрових елементів поділяють на експлуатаційні, економічні, технічні. Експлуатаційні параметри відбивають такі якості елементів, як тривалість безвідмовної роботи, зручність встановлення та демонтажу, габарити, маса і т. і. Економічні параметри характеризують вартість елемента, енергоємність, вміст дорогих і рідкісних матеріалів. Економічні та експлуатаційні параметри використовуються для опису вже реалізованих виробів. На початковому етапі проектування розробник орієнтується загалом на технічні параметри серійних або розроблюваних елементів, оскільки саме технічні параметри визначають можливість реалізації проектованого пристрою в обраному елементному базисі.
 Множину технічних параметрів поділяють на статичні та динамічні. Статичні параметри характеризують властивості і режими роботи елемента у всіх передбачуваних технічними умовами станах.
Множину технічних параметрів поділяють на статичні та динамічні. Статичні параметри характеризують властивості і режими роботи елемента у всіх передбачуваних технічними умовами станах.
Динамічні параметри являють собою обмеження стосовно тривалості перехідних процесів в цифрових елементах і граничні частоти функціонування. Основні динамічні параметри елементів у часовій області показані на рис. 3.1 на прикладі інвертуючого ЛЕ.
Параметри стосовні вхідного сигналу відзначені нижнім індексом "1", а до вихідного сигналу - нижнім індексом "2".
Основні статичні параметри
| Вхідна напруга логічного "0" | 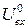 , В , В
|
| Вхідна напруга логічної "1" | 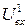 , В , В
|
| Вихідна напруга "0" | 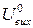 , В , В
|
| Вихідна напруга "1" | 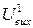 , В , В
|
Логічний перепад 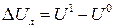
| 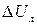 , В , В
|
| Порогова напруга логічного елементу (ЛЕ) | 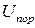 , В , В
|
| Напруга інжектора (для ЕЗЛ) | 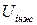 , В , В
|
| Статична завадостійкість "0" - максимально припустима амплітуда позитивної (для позитивної логіки) завади на рівні | 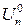 , В , В
|
| Статична завадостійкість "1" - максимально припустима амплітуда негативної (для позитивної логіки) завади на на рівні | 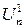 , В , В
|
Статична завадостійкість 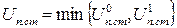
| 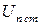 , В , В
|
| Опорна напруга | 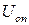 , В , В
|
| Струм споживання від джерела від'ємної і додатної напруги | 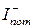 , , 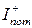 , мА , мА
|
| Вхідний струм "0" | 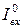 , мА , мА
|
| Вхідний струм "1" | 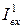 , мА , мА
|
| Вихідний струм "0" | 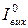 , мА , мА
|
| Вихідний струм "1" | 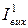 , мА , мА
|
| Потужність споживання у стані "0" | 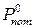 , мВт , мВт
|
| Потужність споживання у стані "1" | 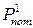 , мВт , мВт
|
Середня потужність споживання: 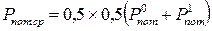
| 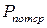 , мВт , мВт
|
Вхідний опір ЛЕ при 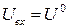
| 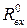 , кОм , кОм
|
Вхідний опір ЛЕ при 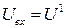
| 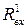 , кОм , кОм
|
Вихідний опір ЛЕ при 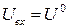
| 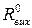 , кОм , кОм
|
Вихідний опір ЛЕ при 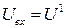
| 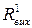 , кОм , кОм
|
| Коефіцієнт розгалужування на виході ЛЕ - максимально припустима кількість підключуваних до виходу аналогічних ЛЕ | 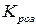
|
| Коефіцієнт об'єднання на вході ЛЕ - максимально припустима кількість аналогічних входів ЛЕ | 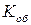
|
| Опір гальванічної розв’язки | 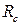 , МОм , МОм
|
Основні динамічні параметри
| Тривалість фронту перемикання сигналу зі стану "0" у стан "1" | 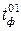
|
| Тривалість фронту перемикання сигналу зі стану "1" у стан "0" | 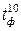
|
Тривалість затримки вимкнення ЛЕ вимірювана від рівня 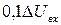 до рівня до рівня 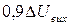
| 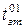
|
Тривалість затримки ввімкнення ЛЕ вимірювана від рівня 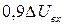 до рівня до рівня 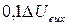
| 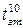
|
Тривалість затримки розповсюдження сигналу при вимкненні логічного елементу, вимірювана від рівня 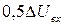 негативного перепаду до рівня негативного перепаду до рівня 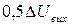 позитивного перепаду позитивного перепаду
| 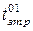
|
Тривалість затримки розповсюдження сигналу при ввімкненні логічного елементу, вимірювана від рівня 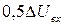 позитивного перепаду до рівня позитивного перепаду до рівня 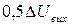 негативного перепаду негативного перепаду
| 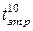
|
Середній час затримки розповсюдження сигналу 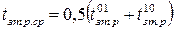
| 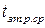
|
Тривалість імпульсу на рівні 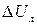
| 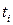
|
| Максимальна робоча частота, на якій у найгірших умовах гарантується працездатність елементу | 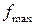
|
| Гранично припустима ємність навантаження | 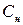
|
| Гранично припустима індуктивність навантаження | 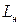
|
Окрім названих основних статичних і динамічних параметрів елементів існує велика кількість специфічних параметрів притаманних ЛЕ певного класу.
Логічні функції
Внаслідок того, що сигнали в цифрових системах представляються двійковими кодами, математичне моделювання таких систем засновано на використанні двозначної логіки, у якій змінні можуть приймати тільки одне з двох значень. Ці значення відповідають двом можливим станам реальних об'єктів (вірне чи помилкове висловлення, висока чи низька напруга, наявність чи відсутність даної ознаки і т.п.). Вони позначаються цифрами 0 і 1, буквами Н (невірно) і І (істинно) чи взагалі будь-якими двома символами, що розрізняються. У технічних додатках звичайно використовуються цифрові позначення, що природним чином зв'язані з двійковими кодами.
У загальному випадку логічні змінні можуть приймати одне зі 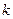 значень (
значень ( 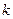 -значна логіка). Перелік усіх
-значна логіка). Перелік усіх 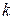 символів, що відповідають області значень, називають алфавітом, а самі символи - буквами цього алфавіту. Логічні функції можуть залежати від однієї, двох і взагалі будь-якого чисел змінних (аргументів). Областю визначення
символів, що відповідають області значень, називають алфавітом, а самі символи - буквами цього алфавіту. Логічні функції можуть залежати від однієї, двох і взагалі будь-якого чисел змінних (аргументів). Областю визначення 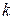 -значної функції від
-значної функції від 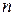 змінних
змінних 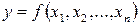 служить безліч наборів
служить безліч наборів 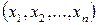 , що є словами довжини
, що є словами довжини 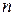 , де кожний з аргументів заміщається буквами
, де кожний з аргументів заміщається буквами 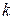 -ічного алфавіту. Тому що кількість усіляких слів довжини
-ічного алфавіту. Тому що кількість усіляких слів довжини 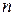 в
в 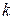 -ічному алфавіті дорівнює кількості різних
-ічному алфавіті дорівнює кількості різних 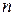 -розрядних чисел з підставою
-розрядних чисел з підставою 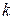 , тобто
, тобто 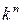 , а кожному такому слову можна зіставити одне із
, а кожному такому слову можна зіставити одне із 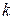 значень, то загальна кількість
значень, то загальна кількість 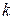 -значних функцій від
-значних функцій від 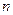 змінних виражається числом
змінних виражається числом 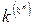 ). Багатозначна логіка має у своєму розпорядженні власний апарат і використовується для математичного моделювання таких об'єктів, компоненти яких характеризуються багатьма станами. Тим часом двозначна логіка поряд із граничною простотою характеризується і достатньою спільністю, тому що до неї можна звести і задачі моделювання багатозначних структур.
). Багатозначна логіка має у своєму розпорядженні власний апарат і використовується для математичного моделювання таких об'єктів, компоненти яких характеризуються багатьма станами. Тим часом двозначна логіка поряд із граничною простотою характеризується і достатньою спільністю, тому що до неї можна звести і задачі моделювання багатозначних структур.
Кількість всіляких двійкових функцій виражається числом 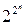 , а область визначення таких функцій являє собою всілякі набори з
, а область визначення таких функцій являє собою всілякі набори з 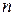 двійкових цифр і їхня загальна кількість дорівнює
двійкових цифр і їхня загальна кількість дорівнює 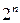 . При збільшенні
. При збільшенні 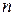 кількість двійкових функцій швидко зростає (при
кількість двійкових функцій швидко зростає (при 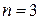 вона дорівнює 256, а при
вона дорівнює 256, а при 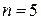 вже перевищує 4 млрд.). Але функції однієї і двох змінних ще можна перелічити і докладно досліджувати, тому що їхня кількість порівняно невелика (4 при
вже перевищує 4 млрд.). Але функції однієї і двох змінних ще можна перелічити і докладно досліджувати, тому що їхня кількість порівняно невелика (4 при 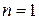 і 16 при
і 16 при 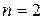 ).
).
Таблиці відповідності
Безліч функцій 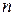 змінних можна представити за допомогою таблиці відповідності, стовпці якого відводяться для
змінних можна представити за допомогою таблиці відповідності, стовпці якого відводяться для 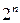 слів довжини
слів довжини 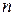 , а рядки - для
, а рядки - для 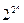 функцій. При цьому номера стовпців визначаються розташованими над ними
функцій. При цьому номера стовпців визначаються розташованими над ними 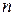 -розрядними двійковими числами, що читаються по вертикалі зверху вниз. Номера функцій ототожнюються з
-розрядними двійковими числами, що читаються по вертикалі зверху вниз. Номера функцій ототожнюються з 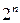 -розрядними двійковими числами, записаними у відповідних рядках таблиці. Таблицю відповідності часто називають також таблицею істинності. Таблиця відповідності для бульових функцій однієї змінної
-розрядними двійковими числами, записаними у відповідних рядках таблиці. Таблицю відповідності часто називають також таблицею істинності. Таблиця відповідності для бульових функцій однієї змінної 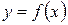 має вид (праворуч зазначені позначення функції)
має вид (праворуч зазначені позначення функції)
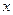
| 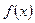
| ||
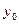
| |||
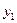
| 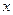
| ||
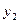
| 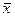
| ||
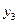
|
Функції 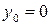 і
і 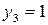 являють собою константи (відповідно тотожний нуль і тотожну одиницю), тому що вони не змінюють своїх значень при зміні аргументу. Функція
являють собою константи (відповідно тотожний нуль і тотожну одиницю), тому що вони не змінюють своїх значень при зміні аргументу. Функція 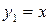 - це повторення, тому що її значення просто збігаються зі значеннями змінної
- це повторення, тому що її значення просто збігаються зі значеннями змінної 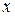 . Єдиною нетривіальною функцією є
. Єдиною нетривіальною функцією є 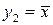 , називана чи запереченням інверсією (читається «не
, називана чи запереченням інверсією (читається «не 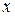 »). Вона дорівнює 1, коли аргумент приймає значення 0, і дорівнює 0 при аргументі 1.
»). Вона дорівнює 1, коли аргумент приймає значення 0, і дорівнює 0 при аргументі 1.
Всілякі 16 функцій двох змінних приведені в табл. 3.1, де зазначені найбільш уживані позначення і назви. Шість із приведених функцій не залежать від чи 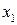 , чи від
, чи від 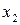 , чи від обох разом. Це константи (
, чи від обох разом. Це константи ( 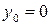 і
і 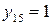 ), повторення (
), повторення ( 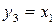 і
і 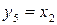 ) і заперечення (
) і заперечення ( 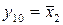 і
і 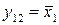 ), що є функціями однієї з змінних (
), що є функціями однієї з змінних ( 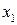 чи
чи 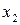 ). Серед інших 10 функцій дві (
). Серед інших 10 функцій дві ( 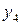 і
і 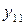 ) відрізняються від відповідних їм функцій (
) відрізняються від відповідних їм функцій ( 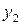 і
і 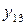 ) лише порядком розташування аргументів. Тому з 16 бульових функцій двох змінних оригінальними є тільки вісім:
) лише порядком розташування аргументів. Тому з 16 бульових функцій двох змінних оригінальними є тільки вісім: 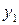 ,
, 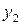 ,
, 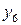 ,
, 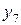 ,
, 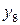 ,
, 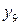 ,
, 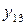 ,
, 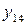 . Можна також помітити, що серед бульових функцій деякого числа змінних містяться усілякі функції меншого числа змінних, котрі називаються виродженими функціями. Так, серед функцій однієї змінної маються дві вироджені - константи 0 і 1, які можна розглядати як функції від нуля змінних. Функції двох змінних містять ті ж константи і чотири функції однієї змінної і т.д.
. Можна також помітити, що серед бульових функцій деякого числа змінних містяться усілякі функції меншого числа змінних, котрі називаються виродженими функціями. Так, серед функцій однієї змінної маються дві вироджені - константи 0 і 1, які можна розглядати як функції від нуля змінних. Функції двох змінних містять ті ж константи і чотири функції однієї змінної і т.д.
Найпростішими компонентами комбінаційної схеми є вентилі, що реалізують елементарні операції. Графічні зображення найбільш вживаних вентилів дані в табл. 3.2 (інверсні входи і виходи позначаються маленькими
Таблиця 3.1
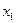
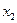
| 0 0 1 1 0 1 0 1 | Позначення | Назви функції | Читання | Бульові формули |
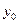
| 0 0 0 0 | Константа 0 | Будь-яке 0 | ||
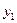
| 0 0 0 1 | 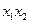 ; ;
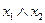
| Коньюнкція | 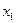 і і 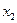
| 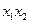
|
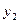
| 0 0 1 0 | 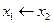
| Заперечення імплікації | 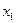 , але не , але не 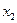
| 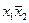
|
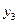
| 0 0 1 1 | 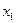
| Повторення 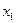
| Як 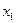
| 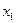
|
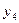
| 0 1 0 0 | 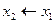
| Заперечення зворотної імплікації | 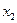 , але не , але не 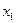
| 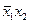
|
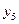
| 0 1 0 1 | 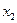
| Повторення 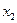
| Як 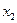
| 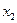
|
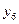
| 0 1 1 0 | 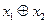
| Сума по модулі 2 | Чи 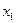 , чи , чи 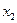
| 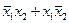
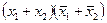
|
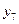
| 0 1 1 1 | 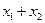 ; ;
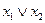
| Диз'юнкція | 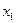 чи чи 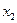
| 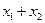
|
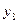
| 1 0 0 0 | 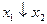
| Стрілка Пірса | Ні 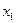 , ні , ні 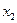
| 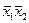
|
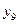
| 1 0 0 1 | 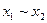
| Еквіваленція | 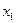 як як 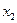
| 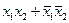
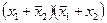
|
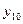
| 1 0 1 0 | 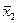
| Заперечення 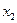
| Не 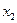
| 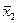
|
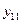
| 1 0 1 1 | 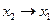
| Зворотна імплікація | Якщо 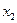 , то , то 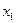
| 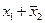
|
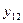
| 1 1 0 0 | 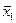
| Заперечення 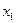
| He 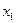
| 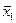
|
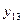
| 1 1 0 1 | 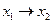
| Імплікація | Якщо 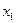 , то , то 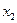
| 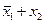
|
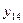
| 1 1 1 0 | 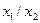
| Штрих Шеффера | не 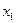 або не або не 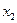
| 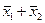
|
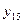
| 1 1 1 1 | Константа 1 | Будь-яке 1 |
кружечками). Як компоненти можуть розглядатися і деякі з'єднання вентилів, що утворять підсхеми. Відповідно говорять про логічне моделювання на різних рівнях - вентильному, реєстровому і т.д. При моделюванні на вентильному рівні логічні формули виражаються в бульовому базисі І, АБО, НІ, тому і логічні схеми звичайно будуються за допомогою аналогічного набору вентилів. Тим часом можуть виявитися зручними і інші вентилі, перетворення до яких забезпечується належною методикою. Зокрема, широко використовуються логічні схеми на основі вентиля І-НІ, що реалізує штрих Шеффера, а також АБО-НІ, що реалізує стрілку Пірса, що припустимо завдяки функціональній повноті кожної з цих операцій.
Таблиця 3.2
| Назва вентиля | Графічні зображення | Бульова формула |
| І (Конюнктор) | 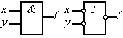
| 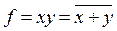
|
| АБО (Дизюнктор) | 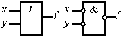
| 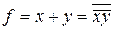
|
| НІ (Інвертор) | 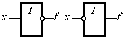
| 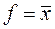
|
| І-НІ (Штрих Шеффера) | 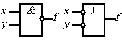
| 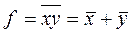
|
| АБО-НІ (Стрілка Пірса) | 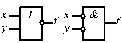
| 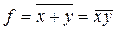
|
| Виключне АБО | 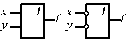
| 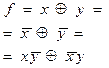
|
| Виключне АБО-НІ | 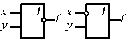
| 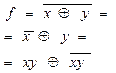
|
| Повторювач | 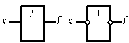
| 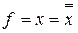
|
Дата добавления: 2015-05-26; просмотров: 706;
