Типи фільтрів
Припустимо, що нам потрібен фільтр низьких частот з плоскою характеристикою в смузі пропускання і різким переходом до смуги придушення. Остаточний нахил характеристики—швидкість спадання вже в смузі замикання — завжди буде 6п дБ/октаву, де п — число «полюсів». На кожен полюс знадобиться один конденсатор або котушка індуктивності, тому вимоги до остаточної швидкості спаду, грубо кажучи, визначають складність фільтру.
Припустимо, що ви вирішили використовувати 6-полюсний фільтр низьких частот. Вам гарантований остаточний спадання 36 дБ/октаву на високих частотах. Тепер можна оптимізувати схему фільтру в сенсі вирівнювання характеристики в смузі пропускання за рахунок зменшення швидкості переходу від смуги пропускання до смуги замикання. З іншого боку, допускаючи деяку нерівномірність характеристики в смузі пропускання, можна добитися крутішого переходу від смуги пропускання до смуги придушення. Третій критерій, який може виявитися важливим, — це здатність фільтру пропускати сигнал із спектром, лежачим в смузі пропускання, без спотворень його форми, фаз, що викликаються зрушеннями. Можна також цікавитися часом наростання, викидом і часом встановлення.
Існують схеми фільтрів, придатні для оптимізації будь-якої з цих характеристик або їх комбінацій. Насправді розумний вибір фільтру відбувається не так, як описано вище; як правило, спочатку задається необхідна рівномірність характеристики в смузі пропускання і необхідне ослаблення на деякій частоті поза смугою пропускання і т.д. Після цього вибирається найбільш відповідна схема з кількістю полюсів, достатньою для того, щоб задовольнялися всі вимоги. У наступних декількох розділах ми розглянемо три широко вживаних типу фільтрів: фільтр Баттерворта (найбільш плоска характеристика в смузі пропускання), фільтр Чебишева (найбільш крутий перехід від смуги пропускання до смуги придушення) і фільтр Бесселя (найбільша постійність часового запізнювання). Будь-який з цих фільтрів може бути реалізований за допомогою різних схем; деякі з них ми пізніше обговоримо. Всі вони рівним чином годяться для побудови фільтрів нижніх частот, верхніх частот і смугових фільтрів.
 Фільтри Баттерворта і Чебишева. Фільтр Баттерворта має найбільш плоску характеристику в смузі пропускання, що досягається ціною зменшення крутизни спаду від смуги пропускання до смуги придушення. Як буде показано далі, у нього також погана фазова характеристика. Амплітудна характеристика задається формулою
Фільтри Баттерворта і Чебишева. Фільтр Баттерворта має найбільш плоску характеристику в смузі пропускання, що досягається ціною зменшення крутизни спаду від смуги пропускання до смуги придушення. Як буде показано далі, у нього також погана фазова характеристика. Амплітудна характеристика задається формулою
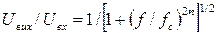 ,
,
де п — порядок фільтру (число полюсів). Збільшення числа полюсів дає можливість зробити плоскішим ділянка характеристики в смузі пропускання і збільшити крутизну спаду від смуги пропускання до смуги придушення, як показано на рис. 2.15.
Застосовуючи фільтр Баттерворта, ми ради максимально плоскої характеристики поступаємося всім іншим. Його характеристика починається горизонтально від нульової частоти і різко спадає вниз на сполучаючій частоті 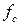 - це частота, відповідна значенню - 3дБ.
- це частота, відповідна значенню - 3дБ.
У більшості додатків найістотнішою обставиною є те, що нерівномірність характеристики в смузі пропускання не повинна перевищувати певної величини, скажемо 1 дБ.
Фільтр Чебишева відповідає цій умові, при цьому допускається нерівномірність характеристики у всій смузі пропускання, але сильно збільшується гострота її зламу. У фільтру Чебишева задаються число полюсів і нерівномірність в смузі пропускання. Допускаючи збільшення нерівномірності в смузі пропускання, одержуємо гостріший злам. Амплітудна характеристика цього фільтру дається формулою
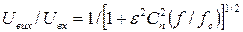
де 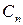 — поліном Чебишева першого роду ступеня
— поліном Чебишева першого роду ступеня 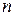 , а
, а 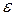 — константа, що визначає нерівномірність характеристики в смузі пропускання. Фільтр Чебишева, як і фільтр Баттерворта, має фазові характеристики, далекі від ідеальних.
— константа, що визначає нерівномірність характеристики в смузі пропускання. Фільтр Чебишева, як і фільтр Баттерворта, має фазові характеристики, далекі від ідеальних.
 На рис. 2.16. представлені для порівняння характеристики 6-полюсних фільтрів нижніх частот Чебишева і Баттерворта. Як легко відмітити, і той, і інший набагато краще за 6-полюсний RС-фільтр.
На рис. 2.16. представлені для порівняння характеристики 6-полюсних фільтрів нижніх частот Чебишева і Баттерворта. Як легко відмітити, і той, і інший набагато краще за 6-полюсний RС-фільтр.
Насправді фільтр Баттерворта з його рівною характеристикою в смузі пропускання не такий привабливий, як це може показатися, оскільки у будь-якому випадку доводиться миритися з деякою нерівномірністю характеристики в смузі пропускання (для фільтру Баттерворта це буде поступове пониження характеристики біля 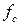 , а для фільтру Чебишева — пульсації, розподілені по всій смузі пропускання). Крім того, активні фільтри, побудовані з елементів, параметри яких витримані з деяким допуском, матимуть характеристику, що відхиляється від розрахункової, а це означає, що насправді на характеристиці фільтру Баттерворта завжди матиме місце деяка нерівномірність в смузі пропускання. На рис. 2.17 проілюстровано вплив найбільш небажаних відхилень значення місткості конденсатора і опору резистора на характеристику фільтру.
, а для фільтру Чебишева — пульсації, розподілені по всій смузі пропускання). Крім того, активні фільтри, побудовані з елементів, параметри яких витримані з деяким допуском, матимуть характеристику, що відхиляється від розрахункової, а це означає, що насправді на характеристиці фільтру Баттерворта завжди матиме місце деяка нерівномірність в смузі пропускання. На рис. 2.17 проілюстровано вплив найбільш небажаних відхилень значення місткості конденсатора і опору резистора на характеристику фільтру.
 В світлі викладеного вельми раціональною конструкцією є фільтр Чебишева. Іноді його називають фільтром рівних пульсації, оскільки його характеристика у області переходу має велику крутизну за рахунок того, що по смузі пропускання розподілено декілька рівновеликих пульсації, число яких зростає разом з порядком фільтру. Навіть при порівняно малих пульсаціях близько 0,1 дБ фільтр Чебишева забезпечує набагато більшу крутизну зламу характеристики, чим фільтр Баттерворта. Щоб виразити цю різницю кількісно, припустимо, що нам потрібен фільтр з не рівномірністю характеристики в смузі пропускання не більше ніж 0,1 дБ і ослабленням 20 дБ на частоті, що відрізняється на 25% від кінцевої частоти смуги пропускання. Розрахунок показує, що для цієї мети потрібен 19-полюсний фільтр Баттерворта або всього лише 8-полюсний фільтр Чебишева.
В світлі викладеного вельми раціональною конструкцією є фільтр Чебишева. Іноді його називають фільтром рівних пульсації, оскільки його характеристика у області переходу має велику крутизну за рахунок того, що по смузі пропускання розподілено декілька рівновеликих пульсації, число яких зростає разом з порядком фільтру. Навіть при порівняно малих пульсаціях близько 0,1 дБ фільтр Чебишева забезпечує набагато більшу крутизну зламу характеристики, чим фільтр Баттерворта. Щоб виразити цю різницю кількісно, припустимо, що нам потрібен фільтр з не рівномірністю характеристики в смузі пропускання не більше ніж 0,1 дБ і ослабленням 20 дБ на частоті, що відрізняється на 25% від кінцевої частоти смуги пропускання. Розрахунок показує, що для цієї мети потрібен 19-полюсний фільтр Баттерворта або всього лише 8-полюсний фільтр Чебишева.
Думка про те, що можна миритися з пульсаціями характеристики в смузі пропускання ради збільшення крутизни перехідної ділянки, доводиться до логічного завершення в ідеї так званого еліптичного фільтру (фільтру Койе), що допускає пульсації характеристики, як в смузі пропускання, так і в смузі придушення ради отримання крутизни перехідної ділянки більшої, ніж навіть у характеристики фільтру Чебишева. За допомогою ЕОМ можна проектувати еліптичні фільтри так само просто, як і класичні фільтри Чебишева і Баттерворта.
 Фільтри Бесселя. Як було вказано раніше, амплітудна характеристика фільтру не дає про нього повної інформації. Фільтр з плоскою амплітудною характеристикою може мати великі зрушення фаз. В результаті цього форма сигналу, спектр якого лежить в смузі пропускання, буде спотворена при проходженні через фільтр. У ситуації, при якій форма сигналу має першорядну вагу, бажано мати в розпорядженні лінійно-фазовий фільтр (фільтр з постійним тимчасовим запізнюванням). Вимога лінійної зміни зрушення фази залежно від частоти еквівалентно вимозі постійності часового запізнювання для сигналу, спектр якого лежить в смузі пропускання, тобто відсутність спотворень форми сигналу. Найбільш плоска ділянка кривої часового запізнювання в смузі пропускання має фільтр Бесселя (також званий фільтром Томсона), подібно тому, як фільтр Баттерворта має найбільш плоску амплітудну характеристику. Щоб зрозуміти, яке поліпшення в тимчасовій області дає фільтр Бесссля, подивіться на рис. 2.18, на якому зображені графіки часового запізнювання для 6-полюсних фільтрів нижніх частот Бесселя і Баттерворта. Погана характеристика часового запізнювання фільтру Баттерворта є причиною ефектів типу викиду при проходженні через фільтр імпульсних сигналів. З іншого боку, за постійність часового запізнювання у фільтру Бесселя доводиться розплачуватися тим, що його амплітудна характеристика має ще пологішу перехідну ділянку між смугою пропускання і смугою замикання, чим характеристика фільтру Баттерворта.
Фільтри Бесселя. Як було вказано раніше, амплітудна характеристика фільтру не дає про нього повної інформації. Фільтр з плоскою амплітудною характеристикою може мати великі зрушення фаз. В результаті цього форма сигналу, спектр якого лежить в смузі пропускання, буде спотворена при проходженні через фільтр. У ситуації, при якій форма сигналу має першорядну вагу, бажано мати в розпорядженні лінійно-фазовий фільтр (фільтр з постійним тимчасовим запізнюванням). Вимога лінійної зміни зрушення фази залежно від частоти еквівалентно вимозі постійності часового запізнювання для сигналу, спектр якого лежить в смузі пропускання, тобто відсутність спотворень форми сигналу. Найбільш плоска ділянка кривої часового запізнювання в смузі пропускання має фільтр Бесселя (також званий фільтром Томсона), подібно тому, як фільтр Баттерворта має найбільш плоску амплітудну характеристику. Щоб зрозуміти, яке поліпшення в тимчасовій області дає фільтр Бесссля, подивіться на рис. 2.18, на якому зображені графіки часового запізнювання для 6-полюсних фільтрів нижніх частот Бесселя і Баттерворта. Погана характеристика часового запізнювання фільтру Баттерворта є причиною ефектів типу викиду при проходженні через фільтр імпульсних сигналів. З іншого боку, за постійність часового запізнювання у фільтру Бесселя доводиться розплачуватися тим, що його амплітудна характеристика має ще пологішу перехідну ділянку між смугою пропускання і смугою замикання, чим характеристика фільтру Баттерворта.
 Існують численні схеми фільтрів, в яких робляться спроби поліпшити тимчасову характеристику фільтру Бесселя, частково жертвуючи постійністю часового запізнювання ради зменшення часу наростання і поліпшення амплітудно-частотної характеристики. Гауссови фільтри мають майже такі ж хороші фазові характеристики, як і фільтри Бесселя, але при покращеній перехідній характеристиці. Інший цікавий клас є фільтри, що дозволяють добитися однакових по величині пульсації кривої часового запізнювання в смузі пропускання аналогічно пульсаціям амплітудної характеристики фільтру Чебишева і що забезпечують приблизно однакове запізнювання для сигналів із спектром аж до смуги придушення. Ще один підхід до створення фільтрів з постійним запізнюванням — це застосування фазових фільтрів, званих інакше фазовирівнюючими. У цих фільтрів амплітудно-частотна характеристика постійна, а зрушення фази може мінятися згідно конкретним вимогам. Тому їх можна застосовувати для вирівнювання часового запізнювання будь-яких фільтрів, зокрема фільтрів Чебишева і Баттерворта.
Існують численні схеми фільтрів, в яких робляться спроби поліпшити тимчасову характеристику фільтру Бесселя, частково жертвуючи постійністю часового запізнювання ради зменшення часу наростання і поліпшення амплітудно-частотної характеристики. Гауссови фільтри мають майже такі ж хороші фазові характеристики, як і фільтри Бесселя, але при покращеній перехідній характеристиці. Інший цікавий клас є фільтри, що дозволяють добитися однакових по величині пульсації кривої часового запізнювання в смузі пропускання аналогічно пульсаціям амплітудної характеристики фільтру Чебишева і що забезпечують приблизно однакове запізнювання для сигналів із спектром аж до смуги придушення. Ще один підхід до створення фільтрів з постійним запізнюванням — це застосування фазових фільтрів, званих інакше фазовирівнюючими. У цих фільтрів амплітудно-частотна характеристика постійна, а зрушення фази може мінятися згідно конкретним вимогам. Тому їх можна застосовувати для вирівнювання часового запізнювання будь-яких фільтрів, зокрема фільтрів Чебишева і Баттерворта.
Порівняння фільтрів. Фільтр Бесселя, не дивлячись на висловлене зауваження про його перехідну характеристику, все ж таки володіє дуже хорошими властивостями в тимчасовій області в порівнянні з фільтру мі Баттерворта і Чебишева. Фільтр Чебишева при його вельми відповідній амплітудно-частотній характеристиці має якнайгірші параметри в тимчасовій області зі всіх цих трьох типів фільтрів. У табл. 2.7. і на рис. 2.19 дана інформація про тимчасові параметри фільтрів цих трьох типів, доповнюючи приведені раніше графіки амплітудно-частотних характеристик. З цих даних можна зробити висновок, що в тих випадках, коли важливі параметри фільтру в тимчасовій області, бажано застосовувати фільтр Бесселя.
Таблиця .2.7.
| f3дБ, Гц | Число полюсів | Час наростання (від 0 до 90%) | Викид, % | Час встановлення, с | Початок смуги подавлення, дБ f=2fc | Ослаблення f=10fc, дБ | ||
| до 1% | до 0,1 % | |||||||
| Фільтр Бесселя (-3дБ при fc=1 Гц) | 1,0 1,0 1,0 1,0 | 0,4 0,5 0,6 0,7 | 0,4 0,8 0,6 0,3 | 0,6 0,7 0,7 0,8 | 1,1 1,2 1,2 1,2 | |||
| Фільтр Бесселя (-3дБ при fc=1 Гц) | 1,0 1,0 1,0 1,0 | 0,4 0,6 0,9 1,1 | 0,8 1,0 1,3 1,6 | 1,7 2,8 3,9 5,1 | ||||
| Фільтр Бесселя (-3дБ при fc=1 Гц) | 1,39 1,09 1,04 1,02 | 0,4 0,7 1,1 1,4 | 1,1 3,0 5,9 8,4 | 1,6 5,4 10,4 16,4 | ||||
| Фільтр Бесселя (-3дБ при fc=1 Гц) | 1,07 1,02 1,01 1,01 | 0,4 0,7 1,1 1,1 | 1,6 4,8 8,2 11,6 | 2,7 8,4 16,3 24,8 |
Дата добавления: 2015-05-26; просмотров: 2348;
