Оценка по критерию К.Пирсона (аналитический метод).

Процесс аналитической оценки закона распределения разбивается на два этапа: построение гистограмм и коммулятивных кривых и проверка допустимости принятого закона распределения отказов по критериям согласия .

Для построения гистограмм и коммулятивных кривых удобно использовать форму, соответствующую таблице 1. Для заполнения данной таблицы вся область предполагаемого распределения разбивается на т равных интервалов (т=10—20). По данным столбца 3 (частота отказов) строится гистограмма, которая аппроксимируется кривой (рисунок 3). Высота каждого прямоуголь­ника соответствует частоте отказов 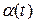в интервале .

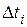Таблица 1 - Форма для построения гистограмм и коммулятивных кривых

Границы интервала	Абсолютная частота отказов	Частота отказов	Накопленная частота отказов	Вероятность безотказной работы	Интенсивность отказов
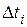
	n ( )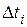

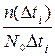
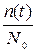
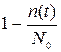
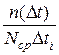
Аналогичные гистограммы можно построить для вероятности безотказной работы (столбец 5 табл.1) и интенсивности отказов (столбец 6). По виду аппроксимирующих кривых устанавливается ориентировочно закон распределения отказов путем сравнения их с теоретическими кривыми.

Рисунок 3 – Гистограмма частоты Рисунок 4 – График накопленных час-отказов тот и соответствующая ему коммулятивная кривая

График накопленных частот и соответствующая ему коммулятивная кривая строятся по данным столбца 4 (рисунок 4). Накопленные частоты получены в результате последовательного сложения следующих друг за другом частот. Высота последней ординаты соответствует объему накоплений всего ряда, или 100%.

Проверка совпадения эмпирической кривой распределения и выбранной теоретической производится по критерию

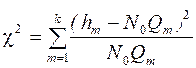, (13)

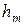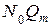где k – число интервалов; и —эмпирическое и теоретическое значения абсолютной частоты отказов; 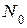— общее число изделий.

Полученные значения критерия х² сравниваются с табличными (приложение) для соответствующего уровня значимости и числа степеней свободы l=k-1.

Если рассчитанное значение х² меньше табличного, то гипотеза об идентичности эмпирического и теоретического законов принимается, в обратном случае гипотеза отвергается и проверяется иной закон.

Основным моментом в определении х² является нахождение разницы между эмпирическим и теоретическим распределением, т. е. 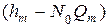.Теоретическая вероятность 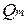указывает долю площади под гауссовой кривой распределения между верхними 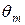и нижними 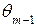границами т-гоинтервала (рисунок 5).

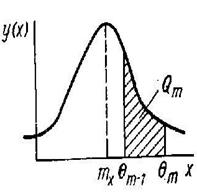
Рисунок 5 – Гауссова кривая распределения отказов

3.2 Графический метод оценки закона распределения Экспериментальные данные записываются в таблицу, где впервый столбец вносятся время 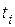отказа испытуемых изделий, во второй — число 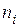изделий, отказавших за данный интервал времени, в третий —накопленное к данному моменту число отказов в четвертый — частость отказов 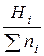, где 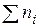— общее число отказов, и в пятый — (1- 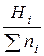). Для графического выявления закона распределения значения 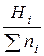или (1- 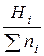) наносят на бумагу со специальной координатной сеткой (вероятностная бумага): с равномерной шкалой для 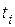по оси абсцисс и логарифмической шкалой по оси ординат при проверке экспоненциального закона распределения (рисунок 6);

- с равномерной шкалой по оси абсцисс и шкалой, соответствующей нормальному закону, по оси ординат при проверке нормального закона распределения;

- с логарифмической шкалой по оси абсцисс и шкалой, соответствующей нормальному закону, по оси ординат при проверке логарифмически-нормального закона распределения;

- со специальными шкалами по осям при проверке закона Вейбулла.

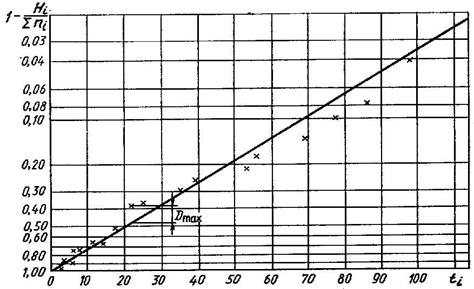
Рисунок 6 – Графическое определение закона распределения

После нанесения точек проводят прямую линию так, чтобы отклонения экспериментальных точек от прямой были бы минимальными и точки располагались по обе стороны от прямой. Наибольшее отклонение D определяется сравнением величин отклонения по оси ординат точек, построенных по экспериментальным данным, от прямой при различных 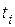и выбором максимального значения. При этом следует помнить о неравномерности шкалы ординат. Затем проверяется соответствие эмпирического и теоретического законов распределения по критерию согласия Колмогорова, который рассчитывается по формуле: 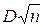,где n — общее число экспериментальных точек. Если 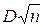<1,0, то гипотеза о пред полагаемом законе подтверждается, если же 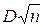>1,0, то гипотеза отвергается.

Если согласие теоретического и эмпирического законов подтверждено, то по графикам можно определить параметры законов распределения. В случае экспоненциального закона значение 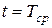соответствует пересечению прямой y=0,37=соnst с интер­поляционной прямой. В случае нормального и логарифмически-нормального законов проводятся прямые y=0,16=соnst и у= =0,84=соnst, проекции точек которых при пересечении с интер­поляционной прямой определят отрезок на оси абсцисс, равный соответственно 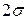и .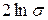

Доверительные нижняя и верхняя границы определяются соответственно из уравнений:

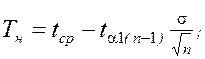(14)

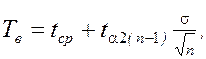(15)

где 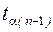— квантиль распределения Стьюдента для вероятности 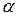и числа степеней свободы f =n-1, находится по таблице (приложение).