Перевод чисел из десятичной системы счисления в любую другую
Для перевода чисел из десятичной с/с в любую другую, необходимо делить десятичное число на основание системы, в которую переводят, сохраняя при этом остатки от каждого деления.
Результат формируется справа налево. Деление продолжается до тех пор, пока результат деления не станет меньше делителя.
Пример 9. Перевести число 13 из десятичной системы счисления в двоичную систему:
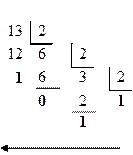
13(10) => 1101(2).
Пример 10. Перевести число 13 из десятичной системы счисления в восьмеричную систему:
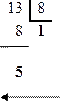
13(10) => 15(8).
Пример 11. Перевести число 638 из десятичной системы счисления в шестнадцатеричную систему:
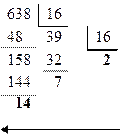
638(10) => 27E(16).
Остатки записываются в шестнадцатеричном виде (14 => Е).
Пример 12. Сложение двоичных чисел:
11011001(2)
+ 1011101(2)
100110110(2).
Для проверки результата сложения двоичное число нужно разбить на триады, перевести в восьмеричную систему счисления согласно таблице 1, а затем перейти в десятичную систему и осуществить сложение.
11 011 001(2)=331(8)=3*82+3*81+1*80=192+24+1=217(10).
1 011 101(2)=135(8)=1*82+3*81+5*80=64+24+5=93(10).
100 110 110(2)=466(8)=4*82+6*81+6*80=256+48+6=310(10).
Проверка:
217(10)+93(10)=310(10).
Пример 13. Сложение шестнадцатеричных чисел:
8E38C(16)
+ 5D35(16)
940C1(16).
Перед сложением необходимо перейти согласно таблице 1 в 10-ю систему счисления, произвести сложение, затем опять вернуться к 16-ой системе счисления.
C(16)+5(16) => 12(10)+5(10)=17(10) => 11(16).
8(16)+3(16)+1(16)=12(10) => С(16).
3(16)+D(16)=3(10)+13(10)=16(10) => 10(16).
E(16)+5(16)+1(16)=14(10)+5(10)+1(10)=20(10) =>14(16).
8(16)+1=9(10) => 9(16).
Вопросы для самоконтроля
- Что такое система счисления?
- Чем характеризуется система счисления?
- Виды систем счисления.
- Десятичная система счисления. Основание. Представление чисел.
- Двоичная система счисления. Основание.
- Восьмеричная и шестнадцатеричная системы счисления.
- Перевод чисел из любой системы счисления в десятичную.
- Перевод чисел из десятичной в любую другую систему счисления.
- Почему для машинной арифметики используется двоичная система счисления?
Методические указания для выполнения практического задания №1. «Системы счисления»
Цель работы: Ознакомиться с системами счислений. Рассмотреть систему представления чисел в памяти ЭВМ.
Задание:
- В приложении 1 выбрать вариант задания.
- Выполнить задание, пользуясь теоретическими сведениями.
- Оформить выполненное задание в тетради для практических занятий.
- Результат работы предъявить преподавателю.
- Ответить на вопросы самоконтроля.
- Защитить выполненную работу у преподавателя.
Приложение 1. Таблица вариантов заданий
| Вариант | Задание |
| |
| |
| |
1 Выполнить действия в двоичной системе счисления:
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
|
2. Алгебра логики
Логика – одна из древнейших наук. Ее основателем считается древнегреческий мыслитель Аристотель (384 – 322гг. до н. э.), который первым систематизировал формы и правила мышления, обстоятельно исследовал категории понятие и суждение, подробно разработал теорию умозаключений и доказательств, описал ряд логических операций, сформулировал основные законы мышления. Он подвергал анализу человеческое мышление, его формы – понятие, суждение, умозаключение, и рассмотрел со стороны строения, структуры. Логика Аристотеля носит название формальной логики. Это название происходит из принципа: правильность рассуждения определяется только его логической формой или структурой и не зависит от конкретного содержания входящих в него высказываний.
Продолжение развития логики связано математической логикой. Основоположником математической логики считается великий математик и философ Готфрид Вильгельм Лейбниц (1646-1716). Он попытался построить первые логические исчисления: арифметические и буквенно-алгебраические. Но Лейбниц высказал только идею, а развил ее окончательно англичанин Джордж Буль (1815-1864). Он вывел для логических построений особую алгебру (алгебру логики). В отличии от обычной логики, в ней символами обозначаются не числа, а высказывания. Алгебра логики (булева алгебра) изучает высказывания, рассматриваемые со стороны их логических значений (истинности или ложности), и логические операции над ними.
Создание алгебры логики представляло собой попытку решать традиционные логические задачи алгебраическими методами. С появлением теории множеств (70-е гг. 19 в.), поглотившей часть первоначального предмета алгебры логики, и дальнейшим развитием математической логики (последняя четверть 19 в. – 1-я половина 20 в.) предмет алгебр логики значительно изменился. Основным предметом алгебры логики стали высказывания. Под высказыванием понимается имеющее смысл языковое выражение, относительно которого можно утверждать, что оно либо истинно, либо ложно.
Пример 1.
- «5 есть простое число». Это высказыванием является истинным.
- «4 + х = 6». Это уравнение не является высказыванием. Однако, придавая переменной х определенное числовое значение, будет высказывание.
- «роза – цветок». Это высказывание является истинным.
- «все углы – прямые». Это высказывание является ложным.
- «3 + 5 = 9». Это высказывание является ложным.
Высказывание считается простым, если никакая его часть не является суждением. Сложное высказывание характеризуется тем, что оно образованно из нескольких высказываний с помощью определенных способов соединения.
Пример 2.
- «Париж – столица Франции». Это высказывание простое.
- «Неверно, что Париж – столица Англии». Это высказывание сложное.
Частные высказывания выражают конкретные факты. Общие высказывания характеризуют свойства групп объектов или явлений.
Пример 3.
- «Луна - спутник Земли». Это частное высказывание.
- «Всякий человек – млекопитающее». Это общее высказывание.
Рассуждение - это цепочка взаимосвязанных высказываний, фактов и общих положений, полученных из других высказываний по определенным правилам вывода.
Пример 4.
- «Если треугольник равносторонний, то у него все углы равны между собой».
- «Если король под шахом и ему некуда ходить, то – мат».
Умозаключение – прием мышления, посредством которого из исходного знания получается новое знание; из одного или нескольких истинных высказываний, называемых предпосылками, по определенным правилам вывода можно получить заключение.
Пример 5. «Все металлы – простые вещества». «Литий – металл». Следовательно «Литий – простое вещество».
Любое правило вывода умозаключений состоит из двух высказываний (простых или сложных). Одно из них называется предпосылкой или условием, а второе – следствием, заключением или выводом.
Пример 6. «Если треугольник равносторонний, то у него все углы 60 градусов». Высказывание «У него все углы равны 60 градусов» – это заключение, а высказывание «Треугольник равносторонний» – это предпосылка.
Существуют умозаключения, осуществляемые по схемам аналогии, индукции и дедукции.
Умозаключение по аналогии – это правило полученное из рассмотрения какого-либо объекта, переносимое на менее изученный, сходный по существенным свойствам и качествам объекта.
Пример 7. Из высказывания «Солнечная система – это планеты, вращающиеся по орбитам, в центре которых находится Солнце» можно получить умозаключение по аналогии: «Атом – это электроны, вращающиеся по орбитам, в центре которых находится ядро».
Индукция – это правило вывода умозаключений при переходе от частных высказываний к общим.
Пример 8. Высказывания: «кошки имеют хвост», «собаки имеют хвост», «обезьяны имеют хвост», «кошки, собаки, обезьяна – млекопитающие». Следовательно, «все млекопитающие имеют хвост». Это умозаключение ложно.
Индуктивный вывод умозаключений позволяет формулировать различные гипотезы, догадки, но иногда он может приводить и к ошибочным умозаключениям.
Дедукция – это правило вывода умозаключений при переходе от общих суждений к частным.
Пример 9. «Умные люди не делают ошибки». «Я – умный человек». Следовательно: «Я не делаю ошибок».
В математической логике не рассматривается конкретное содержание высказывания, важно только, истинно оно или ложно. Поэтому высказывания можно представить некоторой переменной величиной, значением которой может быть только «0» или «1». Если высказывание истинно, то его значение равно «1», если ложно, то равно «0».
Из заданных простых высказываний можно строить более сложные высказывания, используя частицу «не», а также союзы «и», «или», «если..., то...», «тогда и только тогда, когда» и т.п..
Дата добавления: 2015-05-21; просмотров: 4044;
