Логические операции. Истинностные значения новых высказываний определяются при этом только истинностными значениями входящих в них высказываний
Истинностные значения новых высказываний определяются при этом только истинностными значениями входящих в них высказываний. Построение из данных высказываний (или из данного высказывания) нового высказывания называется логической операцией. Знаки логических операций называются логическими связками. Логические связки бывают одноместными (унарными), двухместными (бинарные), трехместными (тернарными) и т.д.
Пример 10.
- Из высказываний «х > 2», «х < 3» при помощи связки «и» можно получить высказывание «x > 2 и х < 3»;
- из высказываний «у > 10», «х < 3» при помощи связки «или» можно получить высказывание «у > 10 или х < 3»;
- из высказываний «х > 2», «у < 3» при помощи связки «если..., то...» можно получить высказывание «если x > 2, то у < 3».
Истинность или ложность получаемых таким образом высказываний зависит от истинности и ложности исходных высказываний и соответствующей трактовки связок как операций над высказываниями.
В алгебре логики логические операции чаще всего описываются при помощи таблиц истинности. В таблице 1 представлена таблица истинности для операции «отрицание» («инверсия»).
Таблица истинности для операции «отрицания»
Таблица 1
| А | не А |
В таблице 2 приведены основные бинарные логические операции и связки.
Основные бинарные логические операции и связки
Таблица 2
| Обозначение логической операции | Другие обозначения логической операции | Название логической операции и связки | Примечание (читается) |
| А1 Ù А2 | А1 & А2 А1 × А2 А1А2 | конъюнкция, логическое умножение, логическое «и» | А1 и А2 |
| А1 Ú А2 | А1 + А2 | дизъюнкция, логическое сложение, логическое «или» | А1 или А2 |
| А1 ® А2 | А1 Ê А2 А1 Þ А2 | импликация, логическое следование | если А1, то А2; А1 имплицирует А2; А1 влечет А2 |
| А1 Å А2 | А1 + А2 А1 Ú А2 А1 D А2 | сумма по модулю 2, разделительная дизъюнкция, разделительное «или» | А1 плюс А2; либо А1, либо А2 |
| А1 ~ А2 | А1 º А2 А1 « А2 А1 Û А2 | эквиваленция, эквивалентность, равнозначность, тождественность | А1 тогда и только тогда, когда А2; А1 эквивалентно А2 |
| А1 ½ А2 | штрих Шеффера, антиконъюнкция | неверно, что А1 и А2; А1 штрих Шеффера А2 | |
| А1 ¯ А2 | А1 °А2
А1 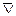 А2 А2
| стрелка Пирса, антидизъюнкция, функция Вебба, функция Даггера | ни А1, ни А2; А1 стрелка Пирса А2 |
Примечание: А1 и А2 являются высказываниями.
Связки и частица «не» рассматриваются в алгебре логики как операции над величинами, принимающими значения 0 (ложь/false) и 1 (истина/true), и результатом применения этих операций также являются числа 0 или 1. В таблице 3 представлены все наборы значений переменных А1 и А2 и значения функций на этих наборах.
Таблица истинности для основных бинарных логических операций
Таблица 3
| А1 | А2 | Ù | Ú | ® | Å | ~ | ½ | ¯ |
Дата добавления: 2015-05-21; просмотров: 782;
