Антидизъюнкция

Результатом операции антидизъюнкции для высказывания А ¯ В будет истинна только тогда, когда оба высказывания ложны.

Пример 17. Высказывания А= «Рим – столица России» и В= «Москва – столица Италии». Сложное высказывание А ¯ В истинно, так как ложны оба высказывания.

Основными символами алгебры логики являются:

• пропозициональные переменные;
• унарная связка Ø и бинарные связки Ù, Ú, ®, ~;
• скобки ( ).

Переменная, значениями которой являются высказывания, называется пропозициональной переменной.

Далее индуктивно вводится понятие формулы, являющееся формализацией понятия «сложного» высказывания. К формуле алгебры логики относят:

• выражение, состоящее только из пропозициональной переменной (А1, В, с);
• выражения, состоящие из пропозициональных формул соединенных связками (Ø С, (А1 Ù А2), (Н1 ® Н2)).

Правила сокращения записей в пропозициональных формулах:

• вместо Ø А пишут ;
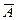• вместо А1 Ù А2 пишут А1А2;
• приоритет применения связок возрастает в следующем порядке

~ ® Ú Ù Ø

• внешние скобки опускаются.

Пример 18.

• ;
• .

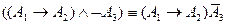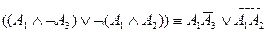Для преобразований формул в равные формулы важную роль в алгебре логики играют следующие равенства:

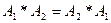1. (закон коммутативности).
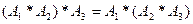2. (закон ассоциативности).
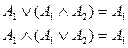3. (закон поглощения).
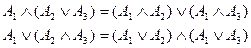4. (закон дистрибутивности).
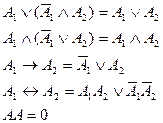5. (закон противоречия).
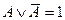6. (закон исключенного третьего);
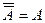7. (закон снятия двойного отрицания);
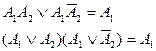8. (закон склеивания);
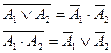9. (закон де Моргана);
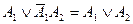10. (закон свертки).

Эти равенства позволяют существенно упростить запись формул освобождением от лишних скобок.